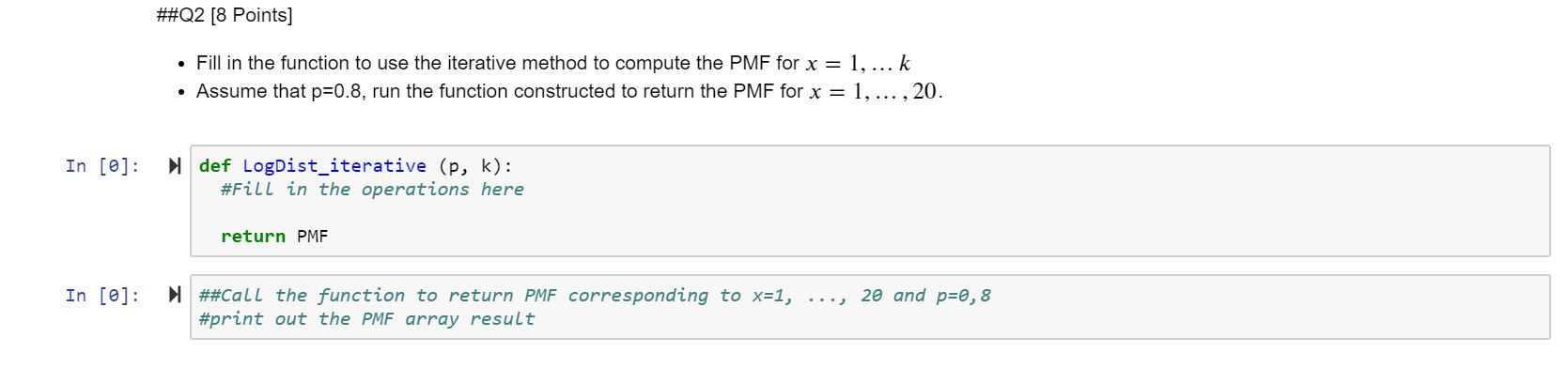
#Exercise 2 [30 Points] ##Setting Logarithmic distribution is a popular distribution in insurance study to model insurance claim frequency. The PMF of logarithmic distribution is as follows: PMF(x) = xln(1 - p) , where x = 1, 2, 3,...,00. -1 The mean of the distribution is equal to - The variance of the distribution is equal to - p+pln(1-p) (1-p) (In(1-P))2 ##Q1 [6 Points] Fill in the function to use the direct method to compute the PMF for x = 1, ... , k. This computation needs to be based on array operations. No loops are allowed. Assume that p=0.8, run the function constructed to return the PMF for x = 1, ... , 20. In [@]: def LogDist_direct (p,k): #Fill in the operations here return PMF In [0]: ##Call the function to return PMF corresponding to x=1, ..., 20 #print out the PMF array result ##Q2 [8 Points] Fill in the function to use the iterative method to compute the PMF for x = 1, ...k Assume that p=0.8, run the function constructed to return the PMF for x = 1, ... , 20. In [0]: def LogDist_iterative (p, k): #Fill in the operations here return PMF In [O]: ##Call the function to return PMF corresponding to x=1, ..., 20 and p=0,8 #print out the PMF array result #Exercise 2 [30 Points] ##Setting Logarithmic distribution is a popular distribution in insurance study to model insurance claim frequency. The PMF of logarithmic distribution is as follows: PMF(x) = xln(1 - p) , where x = 1, 2, 3,...,00. -1 The mean of the distribution is equal to - The variance of the distribution is equal to - p+pln(1-p) (1-p) (In(1-P))2 ##Q1 [6 Points] Fill in the function to use the direct method to compute the PMF for x = 1, ... , k. This computation needs to be based on array operations. No loops are allowed. Assume that p=0.8, run the function constructed to return the PMF for x = 1, ... , 20. In [@]: def LogDist_direct (p,k): #Fill in the operations here return PMF In [0]: ##Call the function to return PMF corresponding to x=1, ..., 20 #print out the PMF array result ##Q2 [8 Points] Fill in the function to use the iterative method to compute the PMF for x = 1, ...k Assume that p=0.8, run the function constructed to return the PMF for x = 1, ... , 20. In [0]: def LogDist_iterative (p, k): #Fill in the operations here return PMF In [O]: ##Call the function to return PMF corresponding to x=1, ..., 20 and p=0,8 #print out the PMF array result