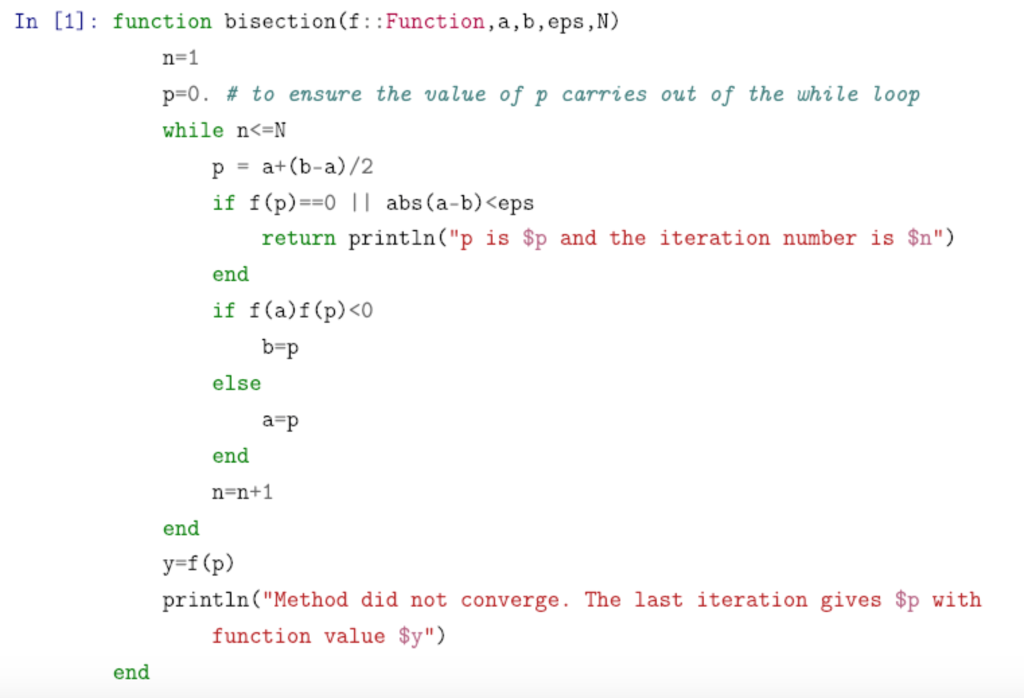
Exercise 2.2-1: Find the root of f(x)4z2 - 10 using the bisection method, with the following specifications a) Modify the Julia code for the bisection method so that the only stopping criterion is whether f(p) -0 (remove the other criterion from the code). Also, add a print statement to the code, so that every time a new p is computed, Julia prints the value of p and the iteration number b) Find the number of iterations N necessary to obtain an accuracy of 104 for the root, using the theoretical results of Section 2.2. (The function f(x) has one real root in (1,2), so set a-1,b 2.) a 1, b 2 in the modified Julia code is used to approximate the actual root, i.e., find |p- PN Compare this error, with the c) Run the code using the value for N obtained in part (b) to compute Pi, P2,.., PN (set d) The actual root, correct to six digits, is p 1.36523. Find the absolute error when pv upper bound for the error used in part (b). In [1]: function bisection(f: Function,a,b,eps, N) n-1 p-o. # to ensure the alue of p carries out of the while loop while n x"5+2x 3-5x-2,0,2,10(-4.),5) Method did not converge. The last iteration gives 1.3125 with function value-0.14562511444091797 Exercise 2.2-1: Find the root of f(x)4z2 - 10 using the bisection method, with the following specifications a) Modify the Julia code for the bisection method so that the only stopping criterion is whether f(p) -0 (remove the other criterion from the code). Also, add a print statement to the code, so that every time a new p is computed, Julia prints the value of p and the iteration number b) Find the number of iterations N necessary to obtain an accuracy of 104 for the root, using the theoretical results of Section 2.2. (The function f(x) has one real root in (1,2), so set a-1,b 2.) a 1, b 2 in the modified Julia code is used to approximate the actual root, i.e., find |p- PN Compare this error, with the c) Run the code using the value for N obtained in part (b) to compute Pi, P2,.., PN (set d) The actual root, correct to six digits, is p 1.36523. Find the absolute error when pv upper bound for the error used in part (b). In [1]: function bisection(f: Function,a,b,eps, N) n-1 p-o. # to ensure the alue of p carries out of the while loop while n x"5+2x 3-5x-2,0,2,10(-4.),5) Method did not converge. The last iteration gives 1.3125 with function value-0.14562511444091797<><>