exercise6.3 b) c) e) f) need helpvery thankful
You can refer to that hints to the exercise a)

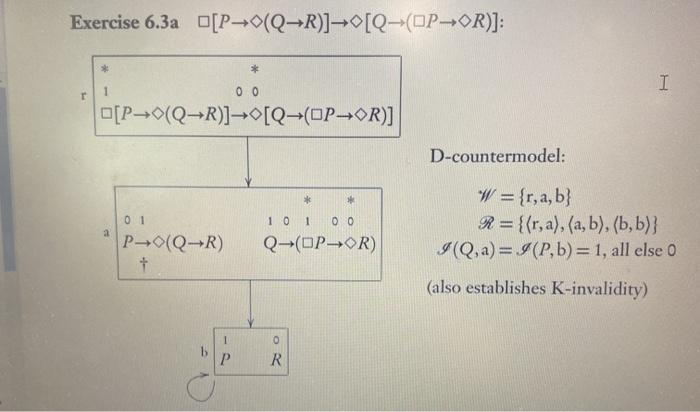
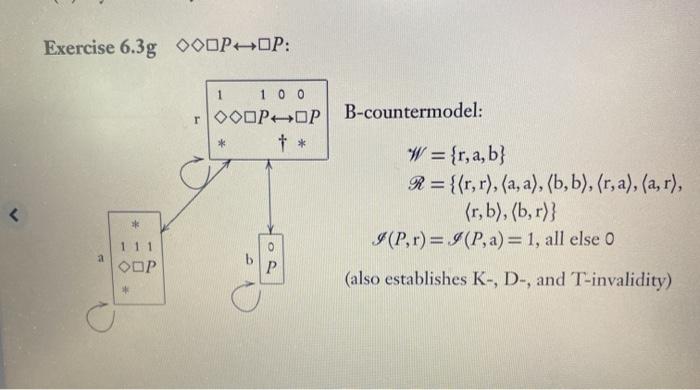
Exercise 6.3 For each of the following wffs, give a countermodel for every system in which it is not valid, and give a semantic validity proof for every system in which it is valid. When you use a single countermodel or validity proof for multiple systems, indicate which systems it is good for. (a)* [P0(QR)]0[Q-OP-OR)] (b) (PAOQO0P-OOQ) (c) (PVOQ)--(OPVOQ) (d)* (PQ-OOPHOQ) (e) (PAQ-00(OP-OQ) (f) DOP-QOOP-OQ) (g)* OOOPOP (h) OOP-OOP (i) O[O(POP)-OP]-(OOP-OP) Exercise 6.3a [P-0(QR)][Q-OP-OR)]: * I 1 00 [P_(Q-R)][Q-(OP-OR)] D-countermodel: * 0 1 PQR) + a W = {r, a, b} R={{r, a),(a, b), (b,b)} I(Q,a)= I (Pb)=1, all else 0 1 0 1 0 0 Q-(OPOR (also establishes K-invalidity) 1 O P R R T-validity proof (also establishes validity in B, S4, and S5): (i) Suppose for reductio that the formula is false in some world r in some T-model (W,R,I). Then V[P-(Q-R)],r)= 1, and... I (ii) ...V[Q-OP-OR)], r) = 0. (iii) By reflexivity, Rrr, so by (ii), V(Q-OP-OR),r)=0. So VOP-OR,r)=0. Thus V(OP,Y)= 1 and so V(P,r)= 1; also... (iv) ...VOR,Y)=0 (v) From(), given Rrr. V(P-0(QR), r) = 1, and so, given (iii), VOQ-R),1)= 1. So for some world "a", Rra and VQ-Ra)= 1. (vi) Since Rra, from (ii) we have V(Q-(OP-OR),a) = 0, and so V(Q,a) = 1; and from (iv) we have V(R. a) = 0. These contradict line (v), Exercise 6.3g OOOPHOP: 1 00 r OOOP-OP B-countermodel: + * W = {r, a, b} R={{r,r), (a, a),(b,b), (r, a),(a, r), (r, b), (b,r)} I(P,r)= I (P, a)= 1, all else o 0 111 ODP P (also establishes K-, D-, and T-invalidity) Answers and Hints 273 1 0 0 TOODPOP + * S4-countermodel: W = {r, a, b} R = {{r,r),(a, a), (b,b), (r, a),(r, b)} I (Pa)= 1, all else 0 1 1 1 OOP S5-validity proof: (1) Given the truth condition for the , it will suffice to show that OOP and OP have the same truth value in every world of every S5-model. So let y be any world in any S5-model, and suppose first for reductio that V(OOOP,r)=1 and ... (ii) ...VOP,r)=0. So for some b, Rrb and V(P,b)=0 (iii) From (i), for some a, Rra and V(ODP,a)= 1, and so for some c, Rac and VOP,c)=1. By symmetry, Rca and Rar, and so by transitivity, Rcb, and so V(P, b)=1, contradicting (ii). So the first reductio assumption is false. Suppose next for reductio that V(OOOP,Y)= 0 and ... (iv) ...VOP,r) = 1. By reflexivity, Rrr. So V(OOP,-) = 1; and so VOODP,Y)= 1, contradicting (iii). Exercise 6.3 For each of the following wffs, give a countermodel for every system in which it is not valid, and give a semantic validity proof for every system in which it is valid. When you use a single countermodel or validity proof for multiple systems, indicate which systems it is good for. (a)* [P0(QR)]0[Q-OP-OR)] (b) (PAOQO0P-OOQ) (c) (PVOQ)--(OPVOQ) (d)* (PQ-OOPHOQ) (e) (PAQ-00(OP-OQ) (f) DOP-QOOP-OQ) (g)* OOOPOP (h) OOP-OOP (i) O[O(POP)-OP]-(OOP-OP) Exercise 6.3a [P-0(QR)][Q-OP-OR)]: * I 1 00 [P_(Q-R)][Q-(OP-OR)] D-countermodel: * 0 1 PQR) + a W = {r, a, b} R={{r, a),(a, b), (b,b)} I(Q,a)= I (Pb)=1, all else 0 1 0 1 0 0 Q-(OPOR (also establishes K-invalidity) 1 O P R R T-validity proof (also establishes validity in B, S4, and S5): (i) Suppose for reductio that the formula is false in some world r in some T-model (W,R,I). Then V[P-(Q-R)],r)= 1, and... I (ii) ...V[Q-OP-OR)], r) = 0. (iii) By reflexivity, Rrr, so by (ii), V(Q-OP-OR),r)=0. So VOP-OR,r)=0. Thus V(OP,Y)= 1 and so V(P,r)= 1; also... (iv) ...VOR,Y)=0 (v) From(), given Rrr. V(P-0(QR), r) = 1, and so, given (iii), VOQ-R),1)= 1. So for some world "a", Rra and VQ-Ra)= 1. (vi) Since Rra, from (ii) we have V(Q-(OP-OR),a) = 0, and so V(Q,a) = 1; and from (iv) we have V(R. a) = 0. These contradict line (v), Exercise 6.3g OOOPHOP: 1 00 r OOOP-OP B-countermodel: + * W = {r, a, b} R={{r,r), (a, a),(b,b), (r, a),(a, r), (r, b), (b,r)} I(P,r)= I (P, a)= 1, all else o 0 111 ODP P (also establishes K-, D-, and T-invalidity) Answers and Hints 273 1 0 0 TOODPOP + * S4-countermodel: W = {r, a, b} R = {{r,r),(a, a), (b,b), (r, a),(r, b)} I (Pa)= 1, all else 0 1 1 1 OOP S5-validity proof: (1) Given the truth condition for the , it will suffice to show that OOP and OP have the same truth value in every world of every S5-model. So let y be any world in any S5-model, and suppose first for reductio that V(OOOP,r)=1 and ... (ii) ...VOP,r)=0. So for some b, Rrb and V(P,b)=0 (iii) From (i), for some a, Rra and V(ODP,a)= 1, and so for some c, Rac and VOP,c)=1. By symmetry, Rca and Rar, and so by transitivity, Rcb, and so V(P, b)=1, contradicting (ii). So the first reductio assumption is false. Suppose next for reductio that V(OOOP,Y)= 0 and ... (iv) ...VOP,r) = 1. By reflexivity, Rrr. So V(OOP,-) = 1; and so VOODP,Y)= 1, contradicting (iii)