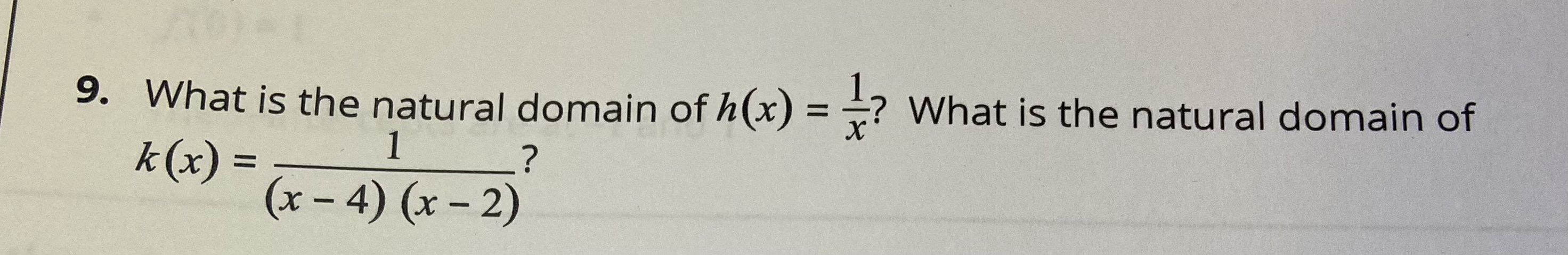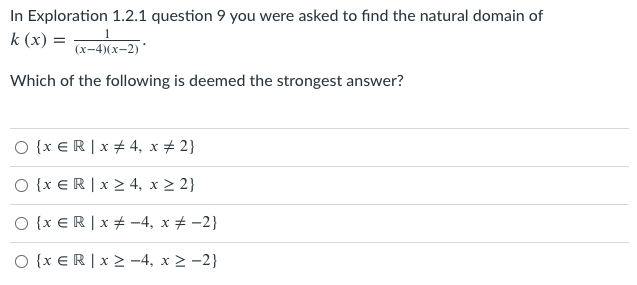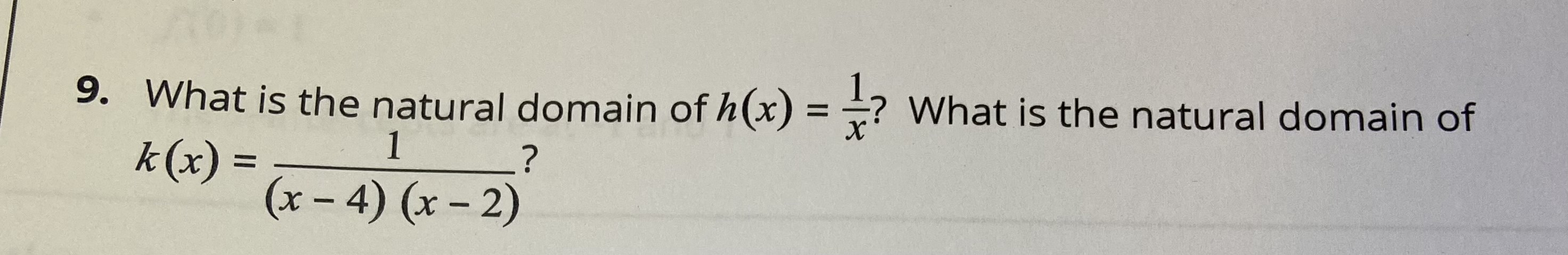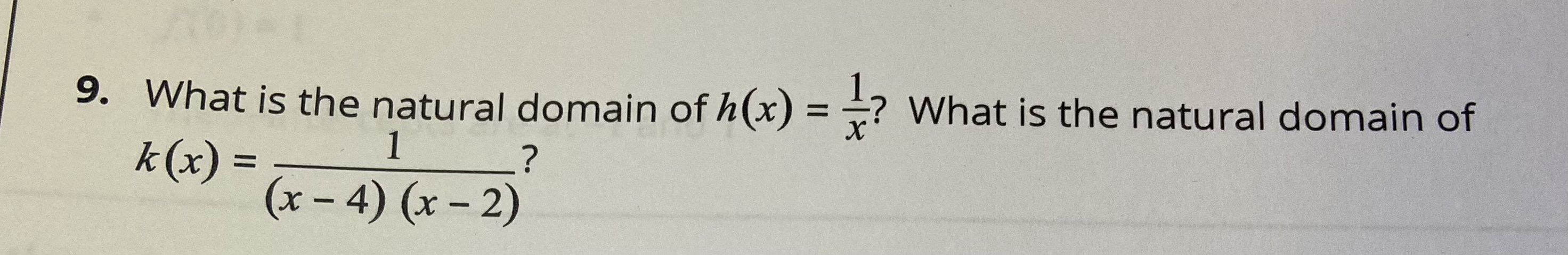



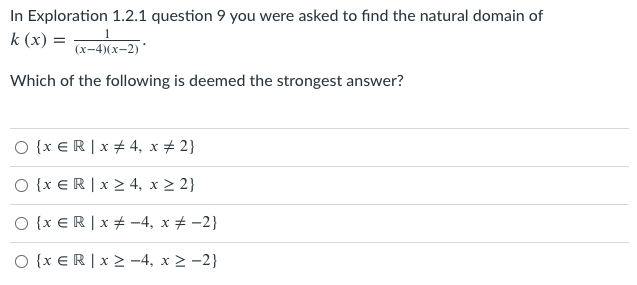



Exploration 1.1.3 question 3:
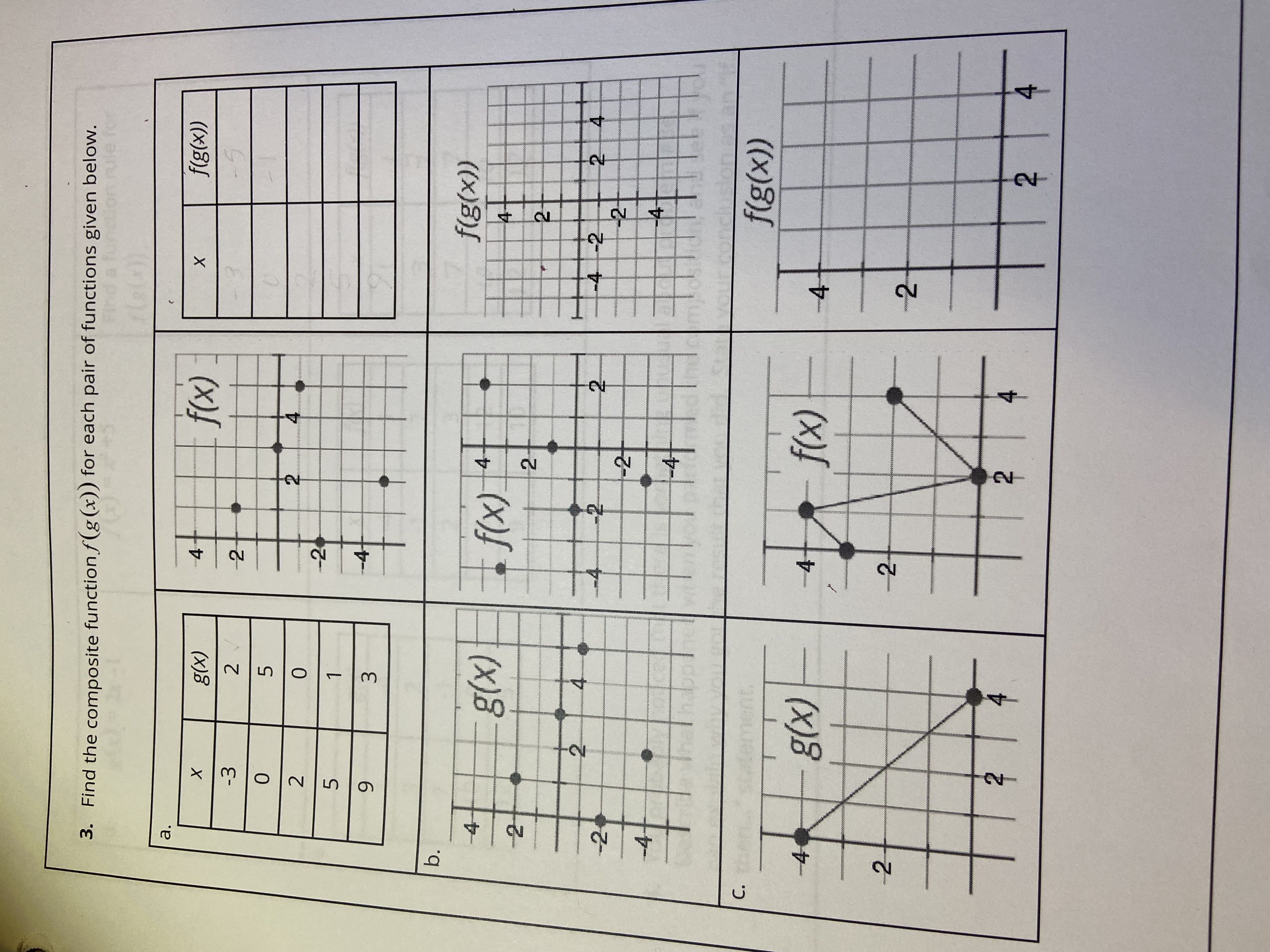
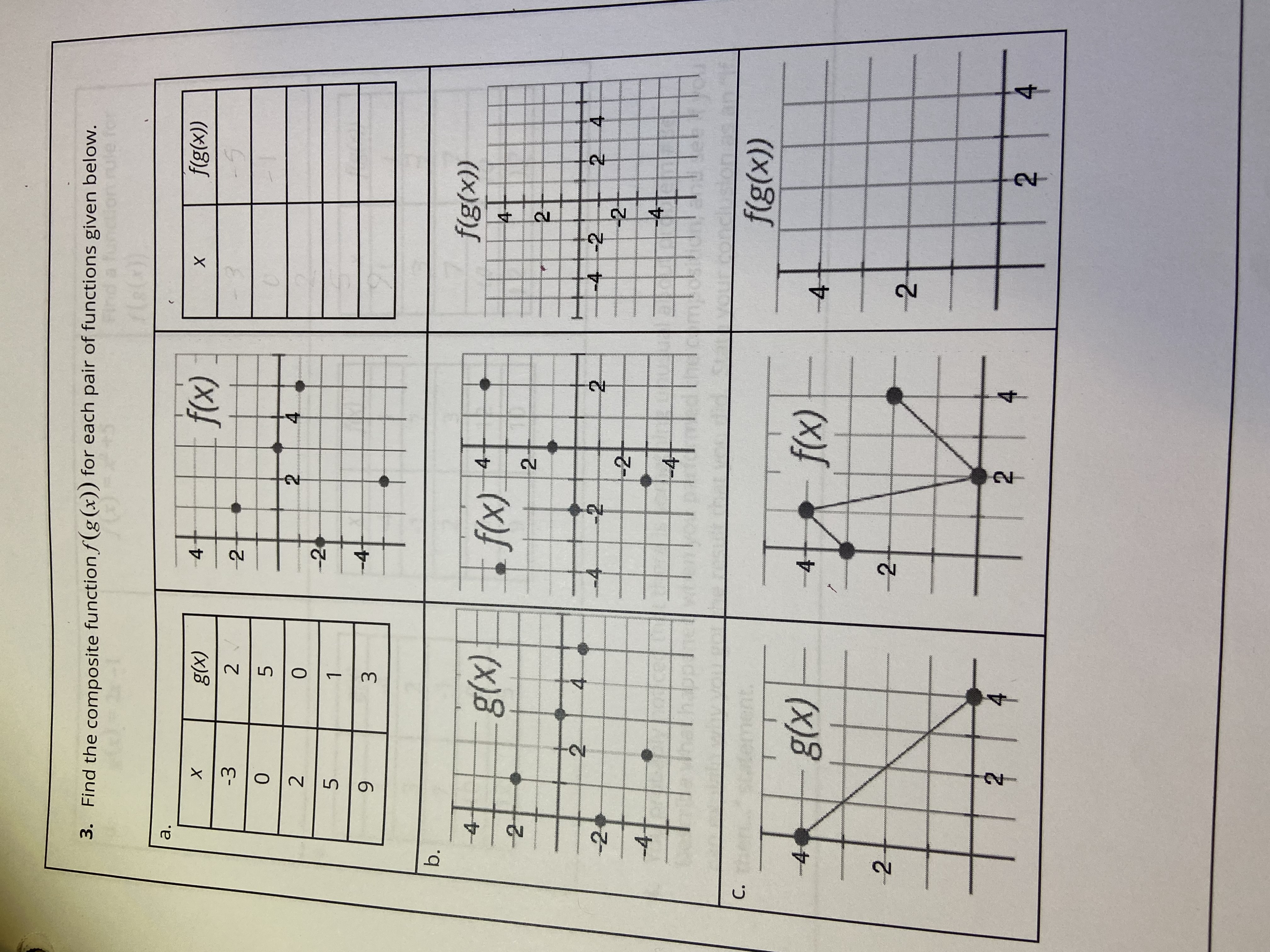
3. Let M be the set of all museums and N the set of all countries. Consider the set of all ordered pairs (m, n) such that museum m is in country n. This can be written symbolically as L = 1(m, n) EMXN the museum m is in the country n) . Is L a function from M to N?9. What is the natural domain of h (x) = ? What is the natural domain of k( x) = 1 ? (x - 4) (x - 2)Exploration 1.2.2: Function Increase and Decrease Consider the definition above and the graph of y = (x - 1)(x - 2)(x -3). with a function of noticesporter based upon the mapping prop 2. Is this graph increasing on [2, 4]?3. Find the composite function f(g (x)) for each pair of functions given below. a X g (x) 4- f ( x ) X fig (x)) - 3 2 3 - 5 UT N O 0 2 1 -2 9 W b. 4 g(x) f ( x ) 1 4 fig(x)) -2- -4 2 2- 2 4 -2 -2 -4 - 2 2 4 -2- -2- C. fig(x)) f (x) 4 2Exploration 1.2.5: Composite Functions - A Cautionary Tale 1. On the same paper, graph the two functions X Z f(x) =-x2+ 8x - 4 on the interval [1, 5] g(x) =-x + 4 on the interval [0, 6] 2. On the same paper, plot the graph of h(x) =f(g(x)) and identify the domain and range of h(x). 3. Verify that f(g(4)) and g(f(4)) are both undefined. What is the lesson to be learned when dealing with composite functions? 4. Find the explicit equation for h(x) =f(g(x)).In Exploration 1.1.3 question 3 you were asked to determine if L is a function from M to N. Assuming. there are no museums that reside on a border between two countries. which of the following would be the strongest answer? C} It is a function because one museum can't be in two different countries. C} It is a function because eyery country has one and only one museum. C} It is not a function because not all countries have a museum. C} It is not a function because some countries have multiples museums. C} It is not a function because it fails the yertical line test. In Exploration 1.2.1 question 9 you were asked to find the natural domain of k (x) = (x-4)(x-2) ' Which of the following is deemed the strongest answer? O {x ER | x # 4, x # 2) O (x ER | x 24, x 2 2) O (xER | x# -4, x # -2) O (xER | x2 -4, x 2-2}In Exploration 1.2.2 you worked on understanding increasing and decreasing functions. Question 2 asked if the graph is increasing on [2,4]. Which of the following is deemed the strongest answer? O It is both increasing and decreasing because when you graph the function, part of the function goes up and part of the function goes down. O The function is increasing because 2 f (2.5) AND 3 f (2.5), therefore by the definition it is decreasing. O The function is increasing because 2