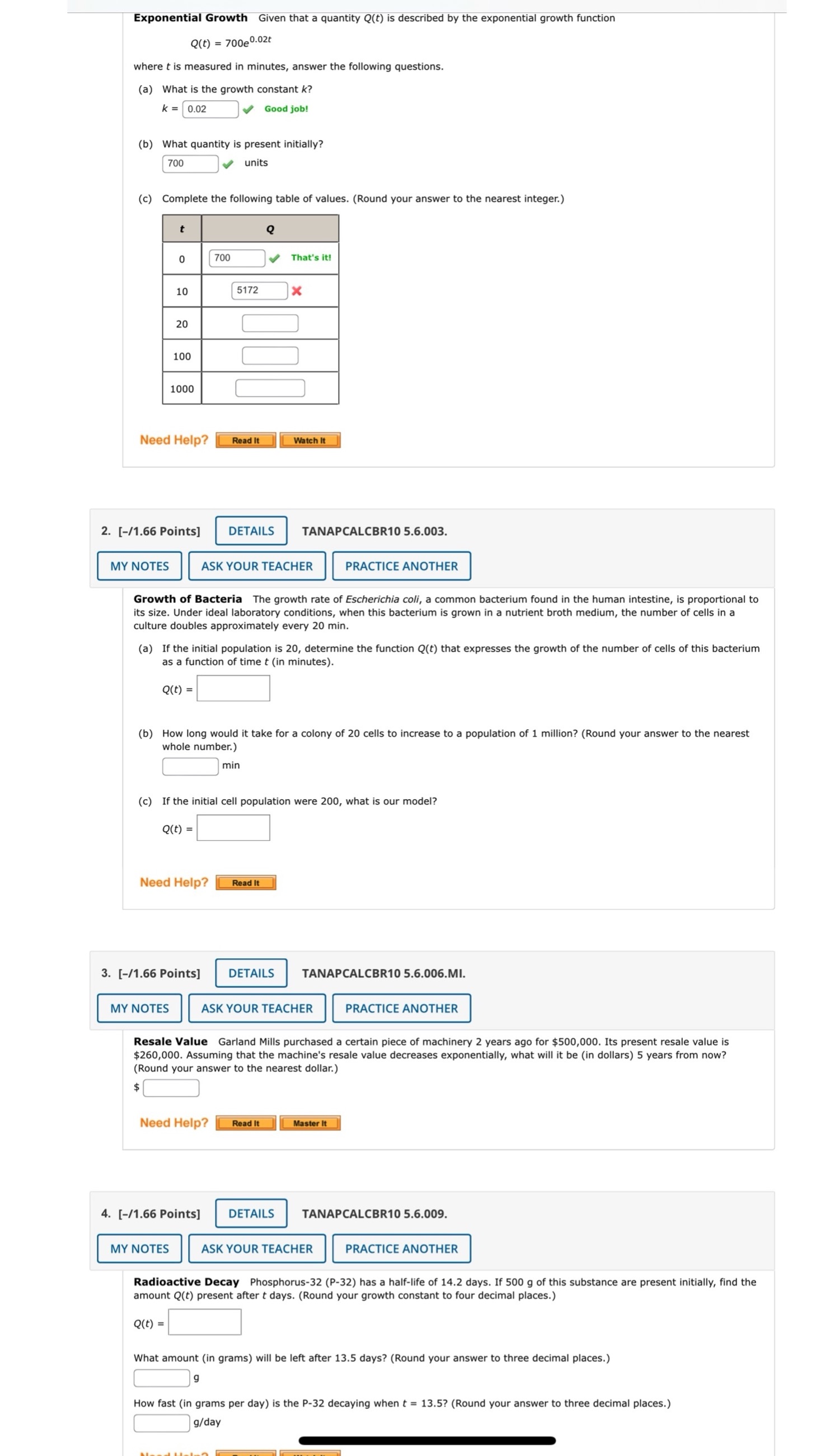
Exponential Growth Given that a quantity Q(t) is described by the exponential growth function Q(t) = 700e 0.02t where t is measured in minutes, answer the following questions. (a) What is the growth constant k? K = 0.02 Good job! (b) What quantity is present initially? 700 units (c) Complete the following table of values. (Round your answer to the nearest integer.) Q 0 700 That's it! 10 5172 X 20 100 1000 Need Help? Read It Watch It 2. [-/1.66 Points] DETAILS TANAPCALCBR10 5.6.003. MY NOTES ASK YOUR TEACHER PRACTICE ANOTHER Growth of Bacteria The growth rate of Escherichia coli, a common bacterium found in the human intestine, is proportional to its size. Under ideal laboratory conditions, when this bacterium is grown in a nutrient broth medium, the number of cells in a culture doubles approximately every 20 min. (a) If the initial population is 20, determine the function Q(t) that expresses the growth of the number of cells of this bacterium as a function of time t (in minutes). 2(t) = (b) How long would it take for a colony of 20 cells to increase to a population of 1 million? (Round your answer to the nearest whole number.) min (c) If the initial cell population were 200, what is our model? Q(t) = Need Help? Read It 3. [-/1.66 Points] DETAILS TANAPCALCBR10 5.6.006.MI. MY NOTES ASK YOUR TEACHER PRACTICE ANOTHER Resale Value Garland Mills purchased a certain piece of machinery 2 years ago for $500,000. Its present resale value is $260,000. Assuming that the machine's resale value decreases exponentially, what will it be (in dollars) 5 years from now? (Round your answer to the nearest dollar.) Need Help? Read it Master It 4. [-/1.66 Points] DETAILS TANAPCALCBR10 5.6.009. MY NOTES ASK YOUR TEACHER PRACTICE ANOTHER Radioactive Decay Phosphorus-32 (P-32) has a half-life of 14.2 days. If 500 g of this substance are present initially, find the amount Q(t) present after t days. (Round your growth constant to four decimal places.) Q(t) = What amount (in grams) will be left after 13.5 days? (Round your answer to three decimal places.) How fast (in grams per day) is the P-32 decaying when t = 13.5? (Round your answer to three decimal places.) 9/day