Expression Trees JAVA

DO NOT CHANGE ANY CODE ONLY MODIFY CODE IN SPECIFIED METHODS IN EXPRESSIONTREE.JAVA

P7/ ??? src ??? ATree.java ??? ExpressionTree.java ??? TestCode.java

Directions

The following UML representation shows the structure of the classes youll be working with:

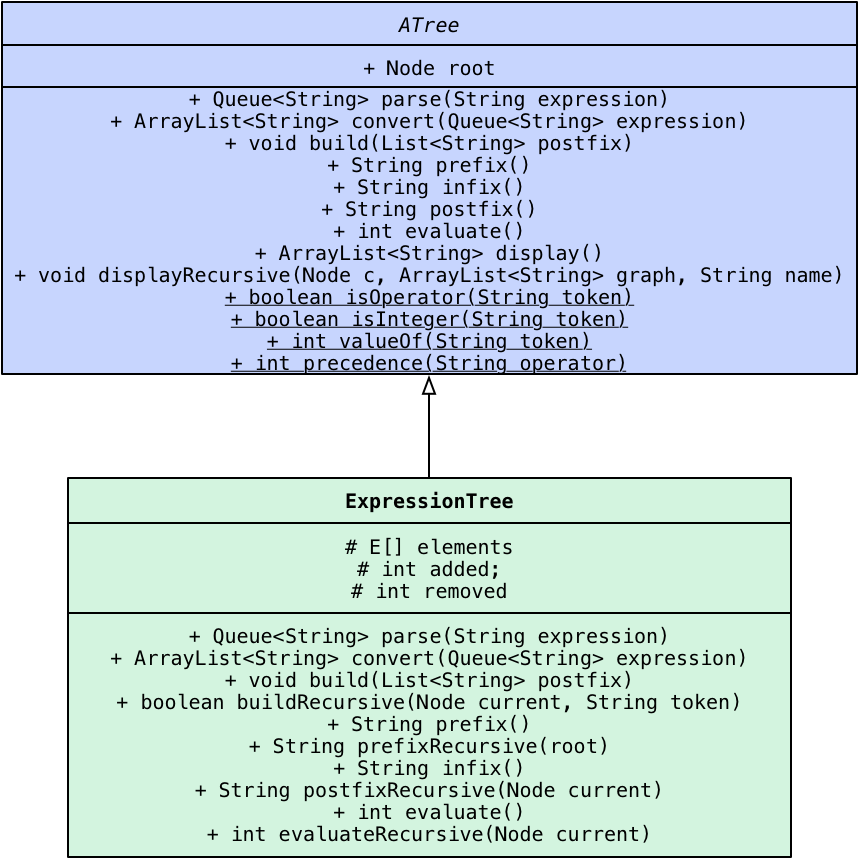
In the ExpressionTree class, implement the following methods (or their corresponding helper methods):

parse method

convert method

build method

prefix method

infix method

postfix method

evaluate method

The TestCode class is provided for testing, and is similar to the code used for automated grading. It takes one command line parameter, which is the expression. You must place the expression in double quotes, for example "3*5+6/2" or "5-3+12/2*(9%5)". The test code calls all of the abstract methods in main. If you want, you can comment out or ignore methods that you have not yet implemented, to allow for incremental development. Here is an example output for the two expressions above:

import java.nio.charset.MalformedInputException; import java.util.ArrayList; import java.util.Deque; import java.util.List; import java.util.Queue;

/** * Provides the Node data structure and defines the abstract methods * that you need to implement in ExpressionTree.java. It also has a * method that converts an expression tree into a format that can be * displayed graphically. * * @author Chris Wilcox * Date: 3/19/2017 * Class: CS165 * Email: wilcox@cs.colostate.edu */ public abstract class ATree {

/** * */ public Node root;

/** * */ public class Node {

/** * */ public String token; /** * */ public Node left; /** * */ public Node right;

/** * * @param value */ public Node(String value) { this.token = value; } }

/** * Parse an infix expression into an {@link ArrayList} of tokens. *

* Reads a string that contains an infix expression, and converts * it to a list of tokens. Each token is an operator, operand (integer), or * parentheses. We suggest using the StringTokenizer method of lexing from the * expressions lab, no changes should be necessary except for the addition of the * modulo operator. The parse method should be able to handle an arbitrary number * of white spaces in the expression. Our implementation of this method is ~8 lines * of code, including brackets but not comments or white space. * @param expression a valid expression * @return expression in infix order */ public abstract Queue parse(String expression);

/** * Convert an infix expression into postfix order. *

* Converts the list of tokens from the parse method from infix to postfix, * using the Shunting-yard algorithm from Edsger Dijkstra, a famous computer * scientist, as documented here. * Our implementation uses {@link Queue} for the queue, and {@link Deque} * for the stack. You may want to use the utility methods {@link #isOperator(String)}, * {@link #isInteger(String)}, and {@link #precedence(String)}. *

* Our implementation is ~21 lines of code. * @param infix expression in infix order * @return expression in postfix order */ public abstract List convert(Queue infix);

/** * Calls a recursive helper method to build an expression tree from a postfix {@link List}. * @param postfix the expression tree */ public abstract void build(List postfix);

/** * Calls a recursive helper method to traverse the expression tree in prefix order and build expression. * @return a string representing the expression in prefix order. */ public abstract String prefix();

/** * Calls a recursive helper method to traverse the expression tree in infix order and build the expression. * @return a string representing the expression infix order. */ public abstract String infix();

/** * Calls a recursive helper method to traverse the expression tree in postfix order and build the expression. * @return a string representing the expression in postfix order. */ public abstract String postfix();

/** * Calls a recursive helper method to evaluate expression tree and return the result. * @return the result of the expression. */ public abstract int evaluate();

/** * Displays the expression tree in graphical format. * @return a dot file representation of the tree. */ public ArrayList display() {

ArrayList graph = new ArrayList(); graph.add("digraph BST {"); graph.add(" ratio = 1.0;"); graph.add(" node [style=filled]"); graph.add(" node [fontname=Arial]"); graph.add(" edge [arrowType=normal]"); graph.add(" edge [fillcolor=orchid]"); displayRecursive(root, graph, "root"); graph.add("}"); return graph; }

/** * * @param current * @param graph * @param name */ public void displayRecursive(Node current, ArrayList graph, String name) { if ((current.left) != null) displayRecursive(current.left, graph, name + "L"); if ((current.right) != null) displayRecursive(current.right, graph, name + "R"); if (isOperator(current.token)) { String operator = current.token; String left = current.left.token; String right = current.right.token; if (operator.equals("%")) operator = "\\%"; if (left.equals("%")) left = "\\%"; if (right.equals("%")) right = "\\%"; // Add node graph.add(" " + name + " [label=\""+operator+"\",shape=square,fillcolor=lightskyblue]"); graph.add(" " + name + " -> " + name + "L"); graph.add(" " + name + " -> " + name + "R"); } else graph.add(" " + name + "[label=\""+current.token+"\",shape=circle,fillcolor=lightseagreen]"); }

// // Utility methods //

/** * @param token a token * @return true if token is an operator. */ public static boolean isOperator(String token) { switch (token) { case "*": case "/": case "%": case "+": case "-": return true; default: return false; } }

/** * @param token a token * @return true if the token is an int. */ public static boolean isInteger(String token) { try { Integer.parseInt(token); return true; } catch (NumberFormatException e) { return false; } }

/** * Converts an {@code String} into an {@code int}. * For example the string "11" is converted to the int 11. * @param token a string representing a number * @return the decimal representation if the token or -1. */ public static int valueOf(String token) { try { return(Integer.parseInt(token)); } catch (NumberFormatException e) { return -1; } }

/** * Returns operator precedence. * @param operator the operator to evaluate * @return a ranking of operator precedence. */ public static int precedence(String operator) { switch (operator) { case "+": case "-": return 2; case "*": case "/": case "%": return 1; default: return 0; } } }

-------------------------------------------------------------------------------------

import java.nio.charset.MalformedInputException; import java.util.*;

/** * */ public class ExpressionTree extends ATree {

public Queue parse(String expression) { Queue infix = new LinkedList(); // YOUR CODE HERE return infix; }

public List convert(Queue infix) { List postfix = new ArrayList(); Deque operators = new ArrayDeque(); // used as a stack // YOUR CODE HERE return postfix; }

@Override public void build(List postfix) { Collections.reverse(postfix); for (String token : postfix) buildRecursive(root, token); }

/** * Builds an expression tree from the postfix representation returned from the convert method. * To build the correct tree, pull tokens from {@code List postfix}, and places * them at the next available node in the tree. * Here is the exact algorithm: *

*

If the tree root is null, create a new node containing the token, * assign it to the root, and return {@code true}. *

If the right child of the current node is null, create a new node * with the token, place it in the right child, and return {@code true}. *

If the right child of the current node is an operator, make a recursive * call passing the right child and token, and return true if successful, * otherwise continue. *

If the left child of the current node is null, create a new node with * the token, place it in the left child, and return {@code true}. *

If the left child of the current node is an operator, make a recursive * call passing the left child and token, and return {@code true} if successful, * otherwise continue. *

If none of the above code returns {@code true}, then the code has failed to add * the token to the tree, so return {@code false}. *

* * Our implementation of the recursive method is ~19 lines of code * @param current the current Node being checked * @param token the token to add * @return {@code true}, if successful */ public boolean buildRecursive(Node current, String token) { // YOUR CODE HERE

return false; }

@Override public String prefix() { return prefixRecursive(root); }

/** * Concatenates the tokens in the expression tree returned from the * {@link #build(List)} method in prefix order. *

* Accumulate the operator first, then the string from the left * and right subtrees. Add an extra space after each token. *

* Our implementation of this method is ~2 lines of code. * @param current the root node * @return the tokens in prefix order */ public String prefixRecursive(Node current) { // YOUR CODE HERE

return ""; }

@Override public String infix() { return infixRecursive(root); }

/** * Concatenates the tokens in the expression tree returned from the * {@link #build(List)} method in infix order. *

*

Accumulate the string from the left subtree *

Add the operator *

Accumulate the string from the right subtree *

* This method should add parentheses to maintain the correct evaluation order, * add a left parentheses before traversing the left subtree, and a right * parentheses after traversing the right subtree. * Do not add any space to the expression string. *

* Our implementation of this method is ~2 lines of code. * @param current * @return the tokens in infix order */ public String infixRecursive(Node current) { // YOUR CODE HERE

return ""; }

@Override public String postfix() { return postfixRecursive(root); }

/** * Concatenates the tokens in the expression tree returned from the * {@link #build(List)} method in postfix order. * First accumulate the string from the left and right subtrees, then add the * operator. Add an extra space after each token. *

* Our implementation of this method is ~2 lines of code. * @param current * @return */ public String postfixRecursive(Node current) { // YOUR CODE HERE

return ""; }

public int evaluate() { return evaluateRecursive(root); }

/** * Traverses the expression tree and produces the correct answer, which should be an integer. * To evaluate, call the recursive version of the method to get the result from the left * subtree, do the same for the right subtree, then combine these two results using the * operator. A case statement based on the operator is needed to perform the arithmetic. *

* Our implementation uses one helper method (~7 lines of code) and is, itself, ~2 lines of code. * @param current * @return */ public int evaluateRecursive(Node current) { // YOUR CODE HERE

return -1; }

}

--------------------------------------------------------------------------

// TestCode.java - test code for expression tree assignment. // Author: Chris Wilcox // Date: 3/19/2017 // Class: CS165 // Email: wilcox@cs.colostate.edu

import java.io.File; import java.io.IOException; import java.io.PrintWriter; import java.nio.charset.MalformedInputException; import java.util.*;

public class TestCode {

// Test code for public static void main(String[] args) throws MalformedInputException{

// Instantiate student code ExpressionTree eTree = new ExpressionTree();

String expression = args[0]; System.out.println("Original Expression: " + expression);

// Verify parse Queue infix = eTree.parse(expression); System.out.println("Infix Tokens: " + infix.toString());

// Verify convert List postfix = eTree.convert(infix); System.out.println("Postfix Tokens: " + postfix.toString());

// Verify build eTree.build(postfix); System.out.println("Build: complete");

// Verify prefix System.out.println("Prefix: " + eTree.prefix());

// Verify infix System.out.println("Infix: " + eTree.infix());

// Verify postfix System.out.println("Postfix: " + eTree.postfix());

// Verify evaluate System.out.println("Evaluate: " + eTree.evaluate());

// Verify display System.out.println("Display: complete"); ArrayList graph = eTree.display(); writeFile(String.format("resources/Graph%s.dot", graph.hashCode()%100), graph); }

// Utility method to write contents of ArrayList to file public static void writeFile(String filename, ArrayList contents) { try { PrintWriter writer = new PrintWriter(new File(filename)); for (String line : contents) writer.println(line); writer.close(); } catch (IOException e) { System.err.println("Cannot write " + filename + "!"); } } }

ATree + Node root +Queue parse(String expression) ArrayList convert (Queue expression) + void build(List postfix) + String prefix) + String infix() + String postfix() + int evaluate() ArrayList display() + void displayRecursive (Node c, ArrayList graph, String name) +boolean_isOperator(String token) +boolean_isInteger(String_token) + int Strin Strin r) ExpressionTree # E[] elements # int added; # int removed +Queue parse(String expression) ArrayList convert (Queue expression) + void build(List postfix) + boolean buildRecursive(Node current, String token) + String prefix) +String prefixRecursive (root) + String infix() + String postfixRecursive (Node current) +int evaluate() + int evaluateRecursive(Node current)