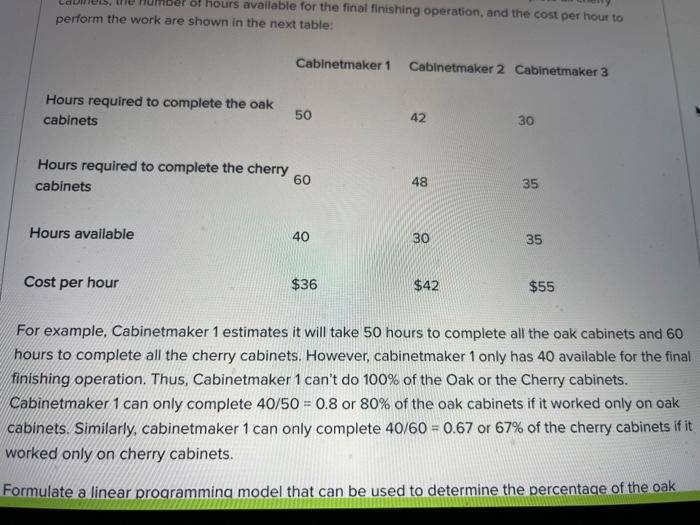
False Friendly reminder: Make sure that decision variables, objective function, and constraints are correct and the model is presented according to the instructions and format indicated on the instructions of this test. You will receive a minimum penalty of 5 points if the model is not 100% correct or if it is not 100% presented as per the instructions. Problem: A well-established manufacturer of cabinets that are sold through local deals across the Bay Area is facing a large backlog of orders of oak and cherry cabinets. In order to find an alternative to fulfill these unserved orders, the company decided to contract with three smaller cabinet makers to do the final finishing operation. For the three cabinet makers, the number of hours required to complete all the oak cabinets, the number of hours required to complete all cherry cabinets, the number of hours available for the final finishing operation, and the cost per hour to perform the work are shown in the next table: Cabinetmaker 1 Cabinetmaker 2 Cabinetmaker 3 hours available for the final finishing operation, and the cost per hour to perform the work are shown in the next table: Cabinetmaker 1 Cabinetmaker 2 Cabinetmaker 3 Hours required to complete the oak cabinets 50 42 30 Hours required to complete the cherry 60 cabinets 48 35 Hours available 40 30 35 Cost per hour $36 $42 $55 For example, Cabinetmaker 1 estimates it will take 50 hours to complete all the oak cabinets and 60 hours to complete all the cherry cabinets. However, cabinetmaker 1 only has 40 available for the final finishing operation. Thus, Cabinetmaker 1 can't do 100% of the Oak or the Cherry cabinets. Cabinetmaker 1 can only complete 40/50 = 0.8 or 80% of the oak cabinets if it worked only on oak cabinets. Similarly, cabinetmaker 1 can only complete 40/60 = 0.67 or 67% of the cherry cabinets if it worked only on cherry cabinets. Formulate a linear programming model that can be used to determine the percentage of the oak Hours required to complete the cherry 60 cabinets 48 35 Hours available 40 30 35 Cost per hour $36 $42 $55 For example, Cabinetmaker 1 estimates it will take 50 hours to complete all the oak cabinets and 60 hours to complete all the cherry cabinets. However, cabinetmaker 1 only has 40 available for the final finishing operation. Thus, Cabinetmaker 1 can't do 100% of the Oak or the Cherry cabinets. Cabinetmaker 1 can only complete 40/50 = 0.8 or 80% of the oak cabinets if it worked only on oak cabinets. Similarly, cabinetmaker 1 can only complete 40/60 = 0.67 or 67% of the cherry cabinets if it worked only on cherry cabinets. Formulate a linear programming model that can be used to determine the percentage of the oak cabinets and the percentage of the cherry cabinets that should be given to each of the three cabinetmakers in order to minimize the total cost of completing both projects. D Question 29 5 pts Clearly indicate and define each one of the decisions variables. Edit View Insert Format Tools Table 12pt Paragraph BI U AT : D Question 30 5 pts Clearly write the Objective Function Edit View Insert Format Tools Table 12pt Paragraph B I A. Tv Question 31 10 pts Clearly include all constraints for the problem. Edit View Insert Format Tools Table 12pt Paragraph B I A T2 : False Friendly reminder: Make sure that decision variables, objective function, and constraints are correct and the model is presented according to the instructions and format indicated on the instructions of this test. You will receive a minimum penalty of 5 points if the model is not 100% correct or if it is not 100% presented as per the instructions. Problem: A well-established manufacturer of cabinets that are sold through local deals across the Bay Area is facing a large backlog of orders of oak and cherry cabinets. In order to find an alternative to fulfill these unserved orders, the company decided to contract with three smaller cabinet makers to do the final finishing operation. For the three cabinet makers, the number of hours required to complete all the oak cabinets, the number of hours required to complete all cherry cabinets, the number of hours available for the final finishing operation, and the cost per hour to perform the work are shown in the next table: Cabinetmaker 1 Cabinetmaker 2 Cabinetmaker 3 hours available for the final finishing operation, and the cost per hour to perform the work are shown in the next table: Cabinetmaker 1 Cabinetmaker 2 Cabinetmaker 3 Hours required to complete the oak cabinets 50 42 30 Hours required to complete the cherry 60 cabinets 48 35 Hours available 40 30 35 Cost per hour $36 $42 $55 For example, Cabinetmaker 1 estimates it will take 50 hours to complete all the oak cabinets and 60 hours to complete all the cherry cabinets. However, cabinetmaker 1 only has 40 available for the final finishing operation. Thus, Cabinetmaker 1 can't do 100% of the Oak or the Cherry cabinets. Cabinetmaker 1 can only complete 40/50 = 0.8 or 80% of the oak cabinets if it worked only on oak cabinets. Similarly, cabinetmaker 1 can only complete 40/60 = 0.67 or 67% of the cherry cabinets if it worked only on cherry cabinets. Formulate a linear programming model that can be used to determine the percentage of the oak Hours required to complete the cherry 60 cabinets 48 35 Hours available 40 30 35 Cost per hour $36 $42 $55 For example, Cabinetmaker 1 estimates it will take 50 hours to complete all the oak cabinets and 60 hours to complete all the cherry cabinets. However, cabinetmaker 1 only has 40 available for the final finishing operation. Thus, Cabinetmaker 1 can't do 100% of the Oak or the Cherry cabinets. Cabinetmaker 1 can only complete 40/50 = 0.8 or 80% of the oak cabinets if it worked only on oak cabinets. Similarly, cabinetmaker 1 can only complete 40/60 = 0.67 or 67% of the cherry cabinets if it worked only on cherry cabinets. Formulate a linear programming model that can be used to determine the percentage of the oak cabinets and the percentage of the cherry cabinets that should be given to each of the three cabinetmakers in order to minimize the total cost of completing both projects. D Question 29 5 pts Clearly indicate and define each one of the decisions variables. Edit View Insert Format Tools Table 12pt Paragraph BI U AT : D Question 30 5 pts Clearly write the Objective Function Edit View Insert Format Tools Table 12pt Paragraph B I A. Tv Question 31 10 pts Clearly include all constraints for the problem. Edit View Insert Format Tools Table 12pt Paragraph B I A T2