fibonaaci recursion analysis

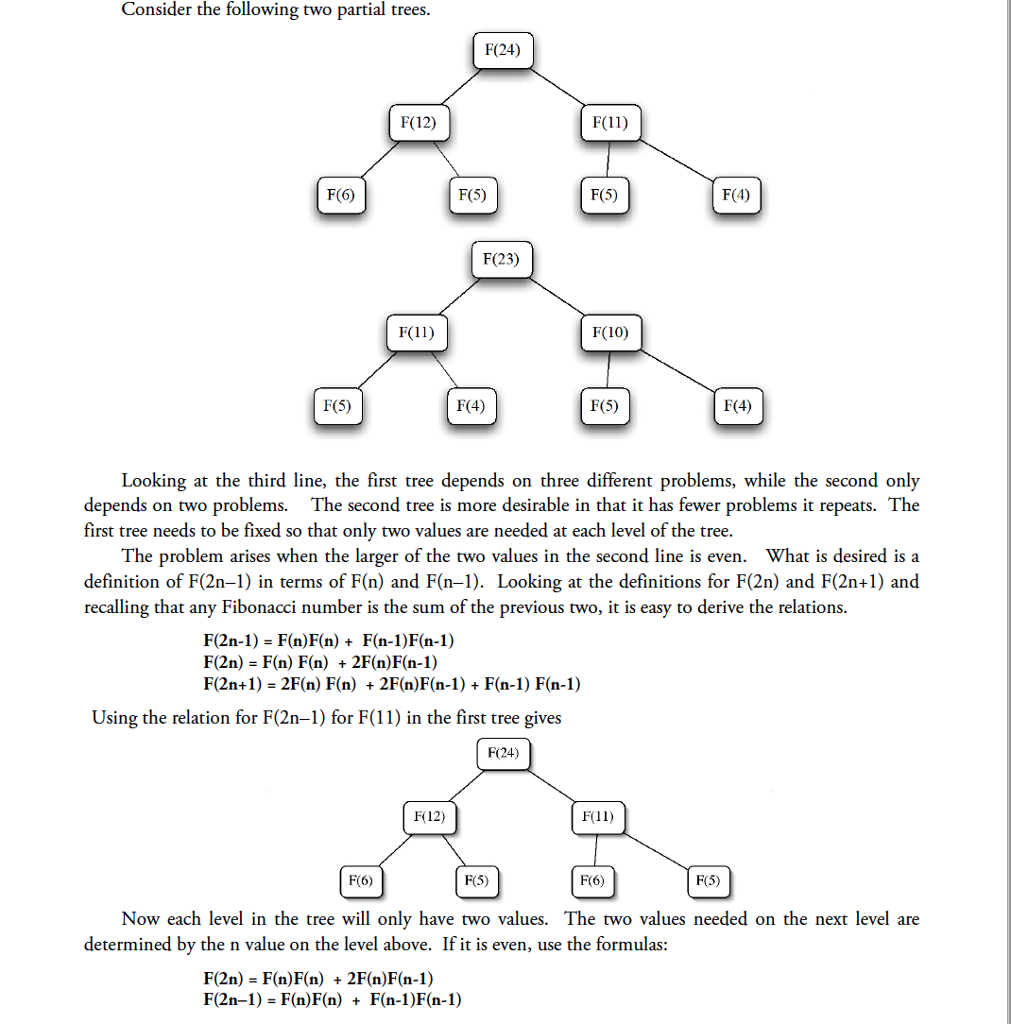
Consider the following two partial trees F(24) F(12) F(11) F(6) F(5) F(5) F(4) F(23) F(11) F(10) F(5) F(4) F(5) F(4) Looking at the third line, the first tree depends on three different problems, while the second only depends on two problems. The second tree is more desirable in that it has fewer problems it repeats. The first tree needs to be fixed so that only two values are needed at each level of the tree The problem arises when the larger of the two values in the second line is even. What is desired is a definition of F(2n-1) in terms of F(n) and F(n-1). Looking at the definitions for F(2n) and F(2n+1) and recalling that any Fibonacci number is the sum of the previous two, it is easy to derive the relation:s F(2n-1) -F(n)F(n) Fn-1)F(n-1) F(2n) = F(n) F(n) + 2F(n)F(n-1) F(2n+1) - 2F(n) F(n) + 2F(n)F(n-1) F(n-1) F(n-1) Using the relation for F(2n-1) for F(11) in the first tree gives F(24) F(12) F(11) F(6) F(5) F6) F(5) Now each level in the tree will only have two values. The two values needed on the next level are determined by the n value on the level above. If it is even, use the formulas F(2n) -F(n)F(n) + 2F(n)F(n-1) F(2n-1) = F(n)F(n) + F(n-1)F(n-1) Consider the following two partial trees F(24) F(12) F(11) F(6) F(5) F(5) F(4) F(23) F(11) F(10) F(5) F(4) F(5) F(4) Looking at the third line, the first tree depends on three different problems, while the second only depends on two problems. The second tree is more desirable in that it has fewer problems it repeats. The first tree needs to be fixed so that only two values are needed at each level of the tree The problem arises when the larger of the two values in the second line is even. What is desired is a definition of F(2n-1) in terms of F(n) and F(n-1). Looking at the definitions for F(2n) and F(2n+1) and recalling that any Fibonacci number is the sum of the previous two, it is easy to derive the relation:s F(2n-1) -F(n)F(n) Fn-1)F(n-1) F(2n) = F(n) F(n) + 2F(n)F(n-1) F(2n+1) - 2F(n) F(n) + 2F(n)F(n-1) F(n-1) F(n-1) Using the relation for F(2n-1) for F(11) in the first tree gives F(24) F(12) F(11) F(6) F(5) F6) F(5) Now each level in the tree will only have two values. The two values needed on the next level are determined by the n value on the level above. If it is even, use the formulas F(2n) -F(n)F(n) + 2F(n)F(n-1) F(2n-1) = F(n)F(n) + F(n-1)F(n-1)