Answered step by step
Verified Expert Solution
Question
1 Approved Answer
Fill in the blanks so that the resulting statement is true. If compound interest is paid four times per year, the compounding period is months




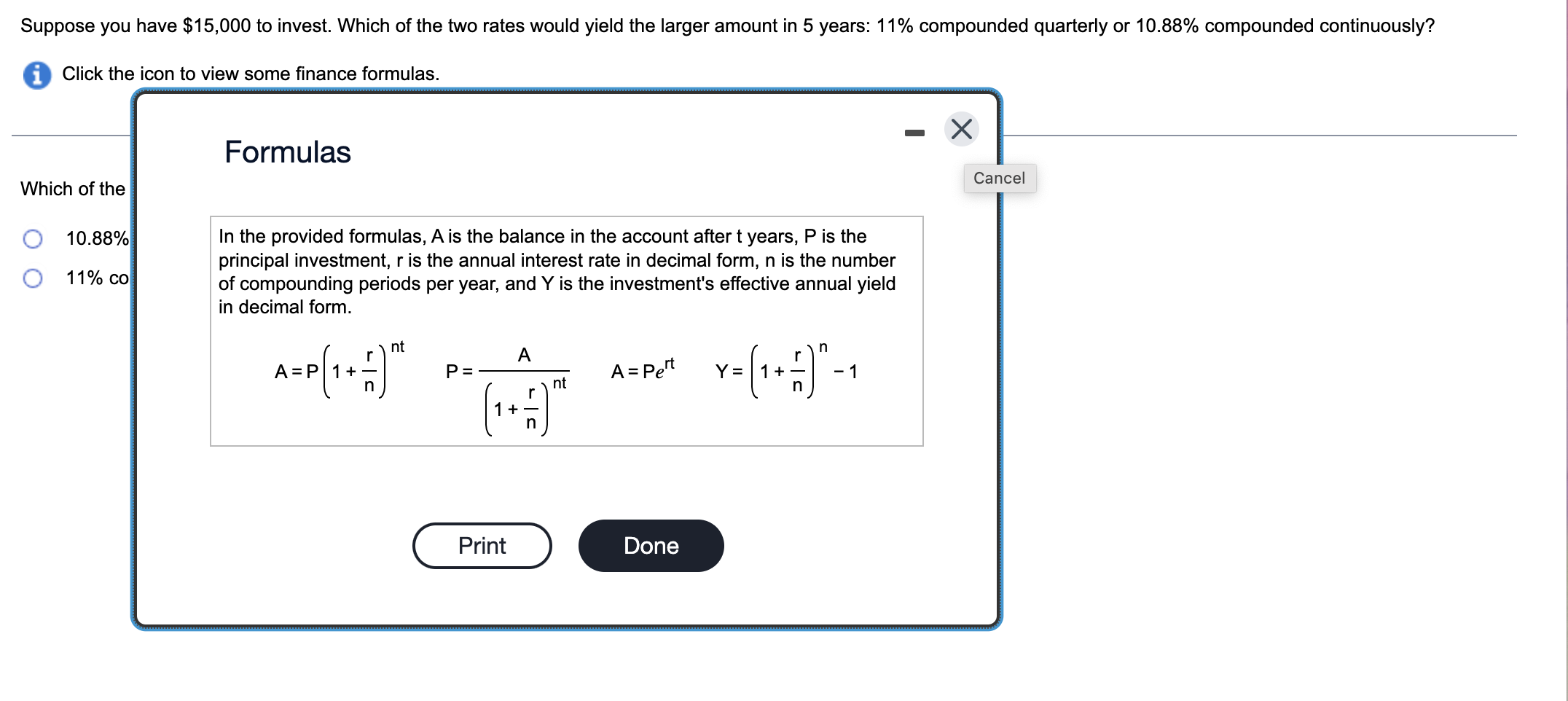


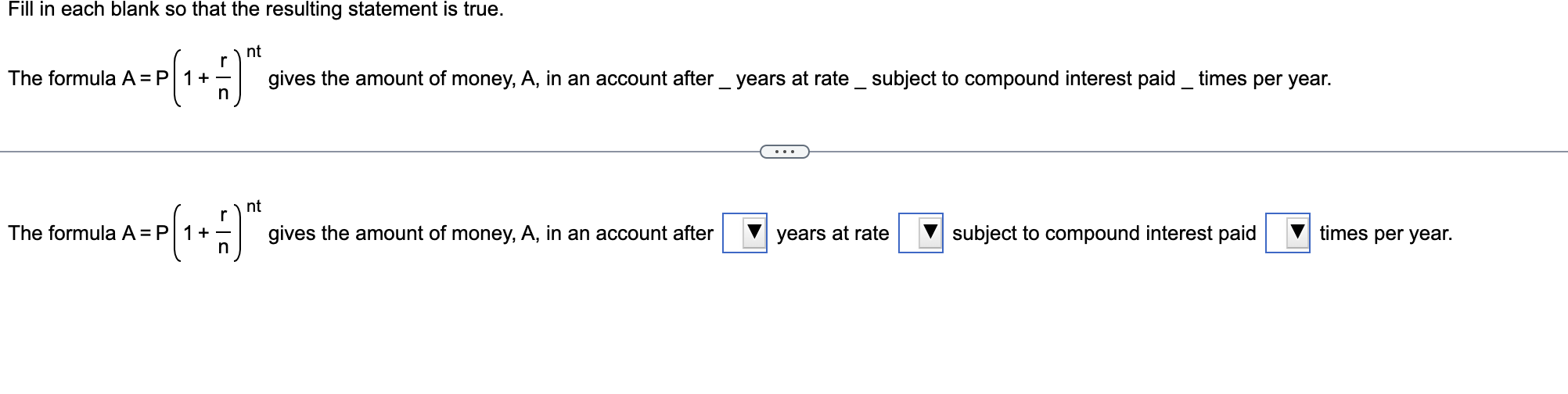

 Fill in the blanks so that the resulting statement is true. If compound interest is paid four times per year, the compounding period is months and the interest is compounded If compound interest is paid four times per year, the compounding period is months and the interest is compounded How much money should be deposited today in an account that earns 3% compounded semiannually so that it will accumulate to $15,000 in three years? Click the icon to view some finance formulas. The amount of money that should be deposited is $ (Round up to the nearest cent.) The principal represents an amount of money deposited in a savings account subject to compound interest at the given rate. A. Find how much money there will be in the account after the given number of years. B. Find the interest earned. Click the icon to view some finance formulas. A. The amount of money in the account after 4 years is $ (Round to the nearest hundredth as needed.) Suppose you have $15,000 to invest. Which of the two rates would yield the larger amount in 5 years: 11% compounded quarterly or 10.88% compounded continuously? Click the icon to view some finance formulas. Formulas Which of the 10.88% In the provided formulas, A is the balance in the account after t years, P is the principal investment, r is the annual interest rate in decimal form, n is the number of compounding periods per year, and Y is the investment's effective annual yield in decimal form. A=P(1+nr)ntP=(1+nr)ntAA=PertY=(1+nr)n1 Click the icon to view some finance formulas. The effective annual yield for a 14% compounded monthly investment is %. (Round to two decimal places as needed.) How much more would you earn in the first investment than in the second investment? $50,000 invested for 50 years at 14% compounded annually $50,000 invested for 50 years at 7% compounded monthly Click the icon to view some finance formulas. You would earn \$ more on the first investment than in the second investment. (Round to the nearest dollar as needed.) Fill in the blanks so that the resulting statement is true. Compound interest is interest computed on the as well as on any accumulated Compound interest is interest computed on the as well as on any accumulated A. Find the future value after one year. B. Use the future value formula for simple interest to determine the effective annual yield. Click the icon to view some finance formulas. A. The future value is $ (Round to the nearest cent as needed.) The principal P is borrowed at a simple interest rate r for a period of time t. Find the loan's future value A, or the total amount due at time t. P=$2000,r=8%,t=3years (Round to the nearest cent as needed.) Fill in each blank so that the resulting statement is true. The formula A=P(1+nr)nt gives the amount of money, A, in an account after_years at rate_subject to compound interest paid_times per year. The formula A=P(1+nr)nt gives the amount of money, A, in an account after years at rate subject to compound interest paid times per year
Fill in the blanks so that the resulting statement is true. If compound interest is paid four times per year, the compounding period is months and the interest is compounded If compound interest is paid four times per year, the compounding period is months and the interest is compounded How much money should be deposited today in an account that earns 3% compounded semiannually so that it will accumulate to $15,000 in three years? Click the icon to view some finance formulas. The amount of money that should be deposited is $ (Round up to the nearest cent.) The principal represents an amount of money deposited in a savings account subject to compound interest at the given rate. A. Find how much money there will be in the account after the given number of years. B. Find the interest earned. Click the icon to view some finance formulas. A. The amount of money in the account after 4 years is $ (Round to the nearest hundredth as needed.) Suppose you have $15,000 to invest. Which of the two rates would yield the larger amount in 5 years: 11% compounded quarterly or 10.88% compounded continuously? Click the icon to view some finance formulas. Formulas Which of the 10.88% In the provided formulas, A is the balance in the account after t years, P is the principal investment, r is the annual interest rate in decimal form, n is the number of compounding periods per year, and Y is the investment's effective annual yield in decimal form. A=P(1+nr)ntP=(1+nr)ntAA=PertY=(1+nr)n1 Click the icon to view some finance formulas. The effective annual yield for a 14% compounded monthly investment is %. (Round to two decimal places as needed.) How much more would you earn in the first investment than in the second investment? $50,000 invested for 50 years at 14% compounded annually $50,000 invested for 50 years at 7% compounded monthly Click the icon to view some finance formulas. You would earn \$ more on the first investment than in the second investment. (Round to the nearest dollar as needed.) Fill in the blanks so that the resulting statement is true. Compound interest is interest computed on the as well as on any accumulated Compound interest is interest computed on the as well as on any accumulated A. Find the future value after one year. B. Use the future value formula for simple interest to determine the effective annual yield. Click the icon to view some finance formulas. A. The future value is $ (Round to the nearest cent as needed.) The principal P is borrowed at a simple interest rate r for a period of time t. Find the loan's future value A, or the total amount due at time t. P=$2000,r=8%,t=3years (Round to the nearest cent as needed.) Fill in each blank so that the resulting statement is true. The formula A=P(1+nr)nt gives the amount of money, A, in an account after_years at rate_subject to compound interest paid_times per year. The formula A=P(1+nr)nt gives the amount of money, A, in an account after years at rate subject to compound interest paid times per year Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


