Answered step by step
Verified Expert Solution
Question
1 Approved Answer
financial mathematics Consider a market model S=(S0,S1,S2) for 3 assets defined on a probability space (,F,P). We assume that S01,S01=S02=1, and St1=k=1t(1+Rk1),St2=k=1t(1+Rk2),t=1,,T, where the returns
financial mathematics 
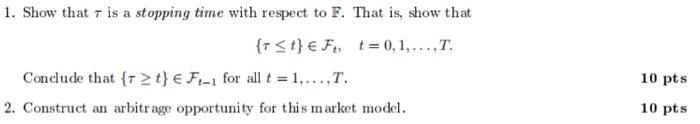
Consider a market model S=(S0,S1,S2) for 3 assets defined on a probability space (,F,P). We assume that S01,S01=S02=1, and St1=k=1t(1+Rk1),St2=k=1t(1+Rk2),t=1,,T, where the returns processes R1=(Rt1)t=1,,T and R2=(Rt2)t=1,,T take values in (1,) and P[Rt2> 0]>0 for all t=1,,T. Let F=(Ft)t=0,,T be the filtration generated by the process (Rt1,Rt2)t=1,,T (with a trivial F0 ). Assume that Rt1=Rt2 for all t1 and that Rt1=2Rt2 for all t, where is the first time when the return of S2 is positive: :=min{t{1,,T}:Rt2>0} with the standard convention that min=. (Note that is a random variable taking values in {1,,T} {}. 1. Show that is a stopping time with respect to F. That is, show that {t}Ft,t=0,1,,T. Conclude that {t}Ft1 for all t=1,,T. 10pts 2. Construct an arbitrage opportunity for this market model. 10pts Consider a market model S=(S0,S1,S2) for 3 assets defined on a probability space (,F,P). We assume that S01,S01=S02=1, and St1=k=1t(1+Rk1),St2=k=1t(1+Rk2),t=1,,T, where the returns processes R1=(Rt1)t=1,,T and R2=(Rt2)t=1,,T take values in (1,) and P[Rt2> 0]>0 for all t=1,,T. Let F=(Ft)t=0,,T be the filtration generated by the process (Rt1,Rt2)t=1,,T (with a trivial F0 ). Assume that Rt1=Rt2 for all t1 and that Rt1=2Rt2 for all t, where is the first time when the return of S2 is positive: :=min{t{1,,T}:Rt2>0} with the standard convention that min=. (Note that is a random variable taking values in {1,,T} {}. 1. Show that is a stopping time with respect to F. That is, show that {t}Ft,t=0,1,,T. Conclude that {t}Ft1 for all t=1,,T. 10pts 2. Construct an arbitrage opportunity for this market model. 10pts 
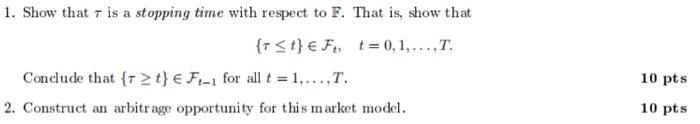
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


