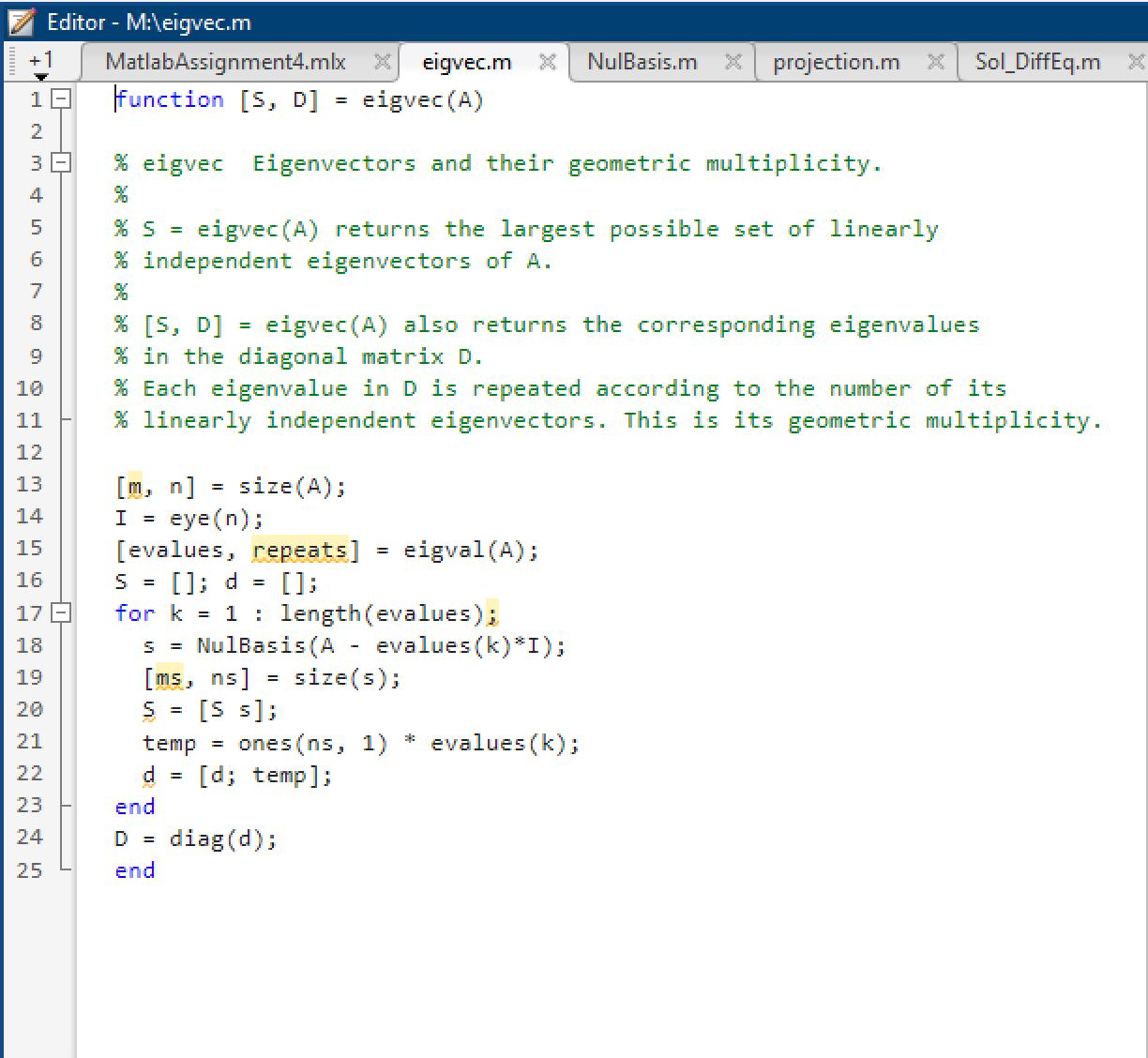
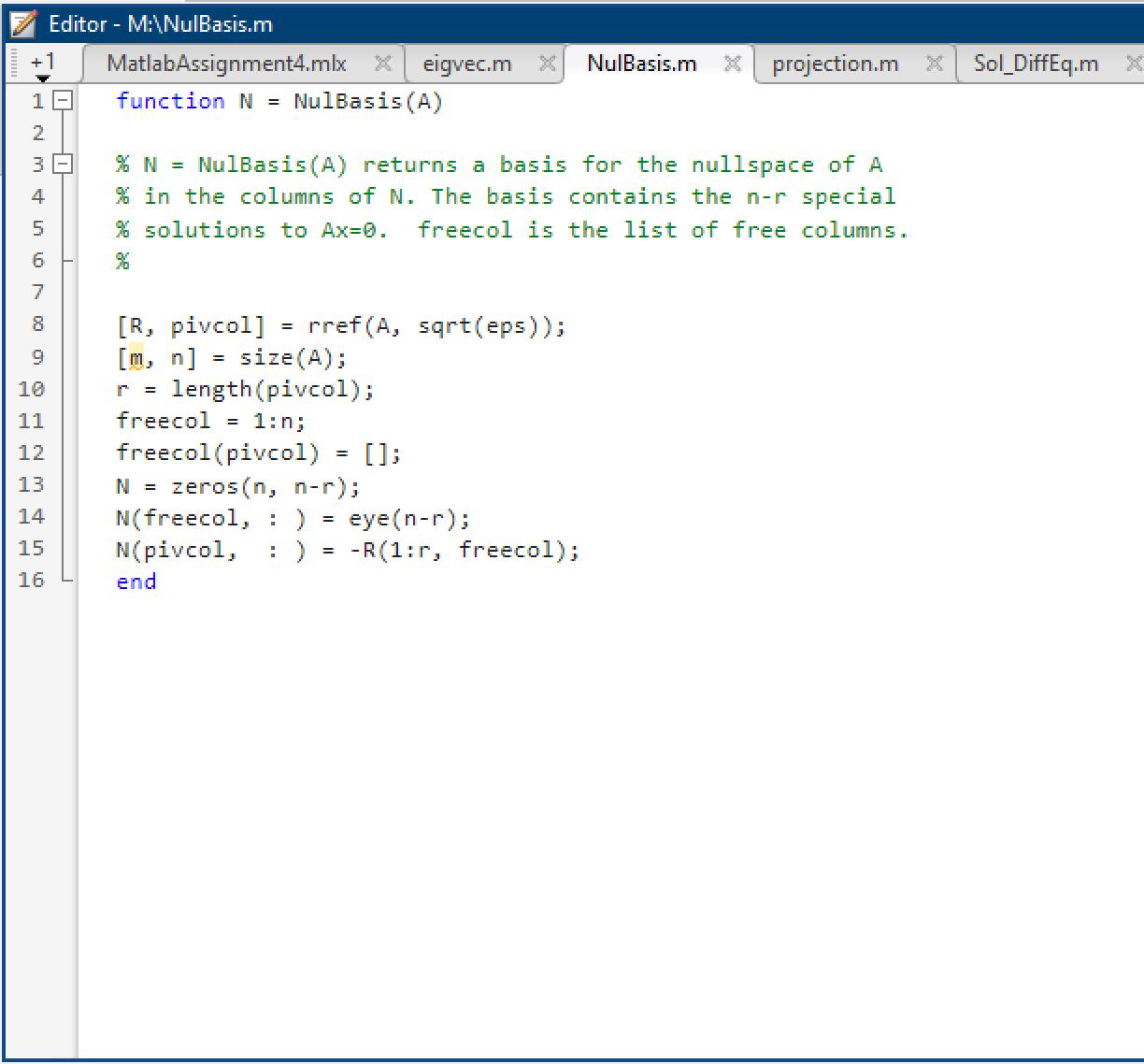
Find eigenvalues and eigenvectors of matrix A and determine if A is diagonalizable. Use the concepts to solve a system of linear differential equations. A. Consider a random 4 x 4 matrix A1: Create and display a 4 x 4 random matrix B with integer entries between -8 and 8 Use the command A1 = tril(B) to create and display matrix A1; what does the command tril return? . Without using MATLAB, can you write down the eigenvalues of A1? State the theorem that you are using. Use the MATLAB built-in function [P, D] = eig (A1); what are matrices P and D?; check if A1*P = P*D and if A1 =P*D*inv(P) STOP! If you do not have A1 = PDP-1, A1 is not diagonalizable. Re-generate another matrix B and repeat the previous commands until you have A1 = PDP-. Call the function eigvec: [P, D] = eigvec (A1); check if A1*P = P*D and if A1 =P*D*inv(P) Note: Compare both commands eig and eigvec. The matrix P obtained by the function eigvec looks nicer. Conclusion: A1 is diagonalizable since A1 = PDP-1. Note that P and D are not unique and find two different decompositions of A1. B. Consider the matrix A2 = Create and display matrix A2. Use the command [P, D] = eig (A2) Check if A2*P = P*D and check if A2 = P*D*inv(P) (ignore the warning message) The m-file function NulBasis (A) returns a basis for the null space of A. Use this function to write a single command that represents a basis for the eigenspace of A2 corresponding to = 5. Conclusion: A2 is not diagonalizable because (provides two different reasons using linear algebra concepts) 5 0 0 0 1 5 0 0 0 01 5 0015 Note: When A*P = P*D, it does not guarantee that A is diagonalizable. C. Consider a linear differential system = 6x1 + 3x2 x = 3x1 + 6x2 Write the above system as x' (t) = Ax(t). Create and display matrix A in MATLAB. . Use the command [P, D] = eigvec (A) Find the dot product of the two eigenvectors of A using the command dot (u, v). DO NOT enter the entires of the eigenvectors manually and use matrix P instead. You will get the dot product = 0. Can you find the relation between the two eigenvectors of A when their dot product is zero? . Solve the system D. Consider a linear differential system. = 4x1 + 2x3 = 2x1 + 3x2 + 4x3 x3 = -2x3 Create and display matrix A. Use the command [P, D] = eigvec (A). Provide a reason why A is diagonalizable. Solve the system Exercise 1 -- Eigenvalues & Eigenvectors 1A Brandi ([-8,8],4,4) % The command tril returns the lower triangular matrix A1 = tril(B) The eigenvalues of A1 are 5, -7, -6, 6, beacuse according to THEOREM HERE since A1 is a triangular matrix its eigenvalues are the entries along the main diagonal. % Find eigenvalues and eigenvectors using eig: % P is (give a description here) % D is (give a description here) [P,D] = eig(A1) % check if A1 = P*D*inv (P) (Yes or No) P*D*inv (P) 0/0/0/0/0/0/0/0/0/0/0 %%%%%%%%%%%%% %%%%%%%% % Check whether P*D*inv(P) = A1. If not, A1 is not diagonalizable. Keep your % previous work, re-generate another matrix B and repeat the process until % A1 is diagonalizable. B = randi ([-8,8],4,4) A1 = tril(B) [P,D] = eig(A1) P*D*inv (P) %%%%%%%%%%%%%%% 9999999/9/9/9/2/9/9/0/0/0/0 % Find eigenvalues and eigenvectors using eigvec: [P,D] = eigvec (A1) % check if A1 = P*D*inv (P)? (Yes or No) P*D*inv(P) Conclusion: A1 is diagonalizable since A = PDP-. Note that P and D are not unique. Decompose A1 using two different sets of P and D. A1 = *inv(P) HIE A1 = *inv(P) 1 XXXXXX 1B %A2 = % [P,D] = eig (A2) % check if A2*P = P*D % check if A2 = P*D*inv (P) % write a single command for a basis of the eigenspace of A2 corresponding % to lambda = 5 using NulBasis Conclusion: A2 is NOT diagonalizable because (using P*D*inv(P)) (using the dimension of the eigenspace) 1C . %A = %[P,D] = eigvec (A) %dot (,) Let v1 and v2 be two linearly indepedent eigenvectors of A. v1 and v2 are zero. The solution to the system 1D x = 6x + 3x = 3x1 + 6x2 "[]+G[]. is X(t) = ce %A = %[P,D] eigvec (A) A is diagonalizable because (provide a reason using matrix P) 2 x = 4x1 + 2x3 The solution to the system x = 2x1 + 3x2 + 4x3 is x(t) = ce x = -2x3 because their dot product is 14 Editor - M:\eigvec.m +1 MatlabAssignment4.mlx X eigvec.m X function [S, D] = eigvec (A) 1 Min 00 22 % eigvec Eigenvectors and their geometric multiplicity. % % S = eigvec (A) returns the largest possible set of linearly 6 % independent eigenvectors of A. 7 4 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 % [S, D] % in the diagonal matrix D. % Each eigenvalue in D is repeated according to the number of its % linearly independent eigenvectors. This is its geometric multiplicity. = [m, n] = size (A); I = eye(n); [evalues, repeats] []; d []; eigvec (A) also returns the corresponding eigenvalues [ms, ns] S = S = for k=1: length (evalues); = = NulBasis (A - evalues (k)*I); size(s); = eigval(A); d end D = diag(d); end NulBasis.m [S s]; temp = ones (ns, 1) * evalues (k); [d; temp]; projection.m X Sol_DiffEq.m X Editor - M:\NulBasis.m +1 MatlabAssignment4.mlx X eigvec.m X function N = NulBasis (A) 1- 2 3 4 5 6 9 10 11 12 13 14 15 16 % N = NulBasis (A) returns a basis for the nullspace of A % in the columns of N. The basis contains the n-r special % solutions to Ax=0. freecol is the list of free columns. [R, pivcol] [m, n] = size (A); r = length (pivcol); = rref (A, sqrt(eps)); freecol = 1:n; freecol (pivcol) []; N = zeros(n, n-r); N(freecol, :) eye(n-r); N(pivcol, end NulBasis.m X projection.m X Sol_DiffEq.m X -R(1:r, freecol);