find the answer

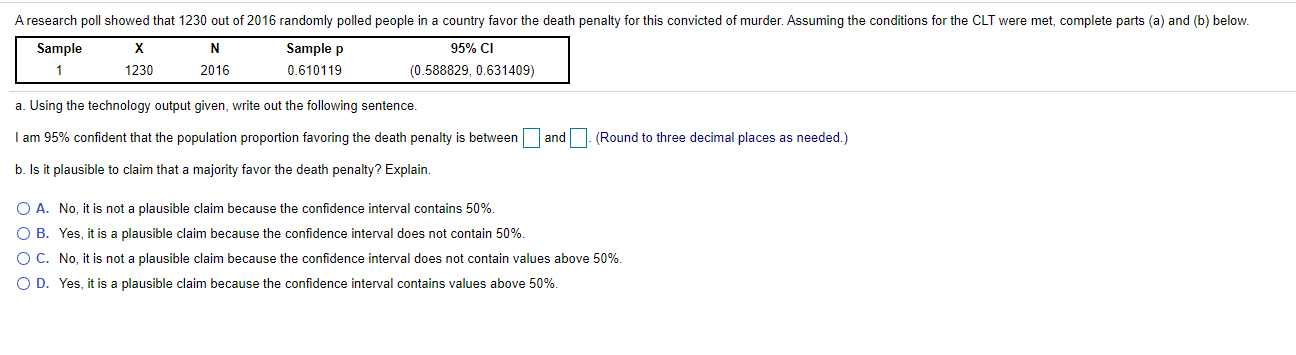
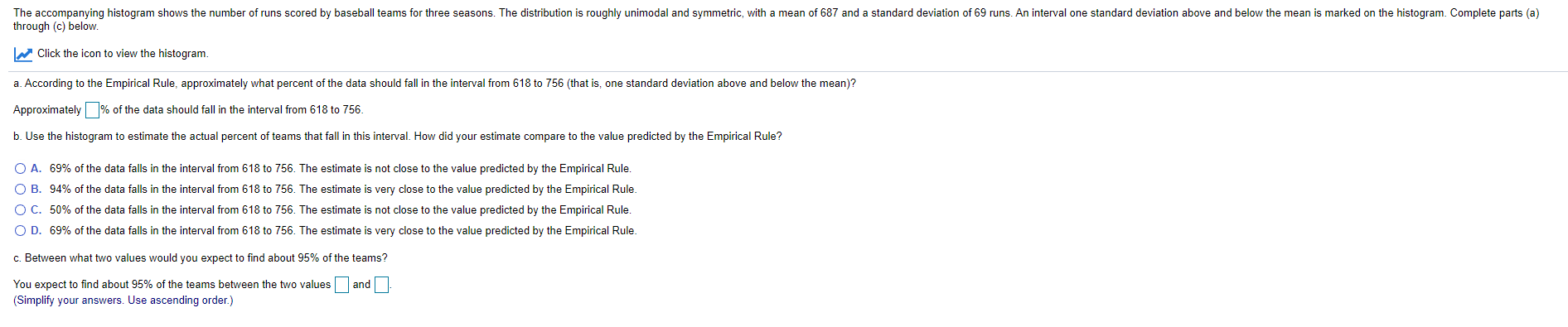
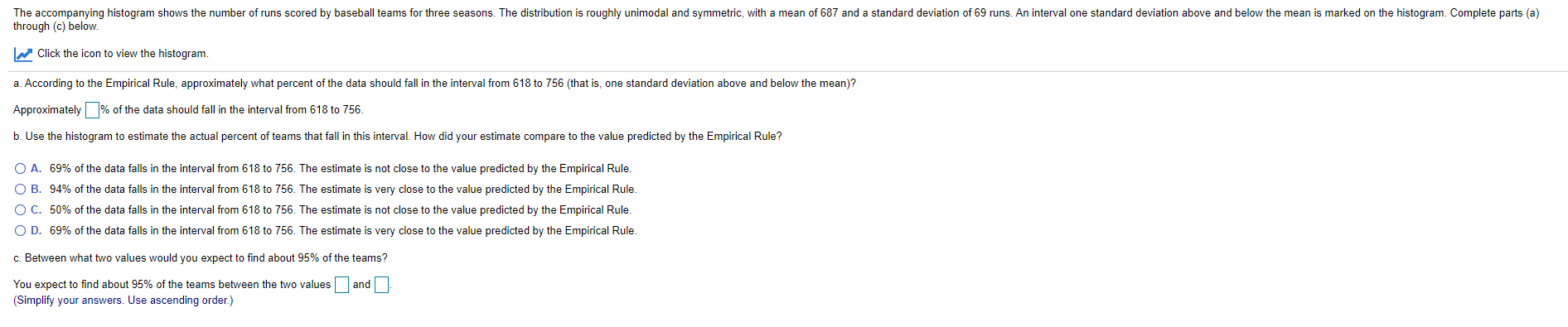
A raearch poll showed that 1230 out of 2016 randomlyr polled people in a country favor the death penalty for this convicted of murder. Assuming the conditions for the CLT were met, complete parts (a) and {b} below. Sample X N Sample [1 95'!- CI 1 1230 2016 0.510119 (0.533629, 0.631409) a. Using the technology output given, write out the tollowing sentence. I am 95% condentthat the population proportion favon'ng the death penalty is between and . (Round to three decimal places as needed.) b. is it plausible to claim that. a majority favor the death penalty? Explain. O A. No. it is not a plausible claim because the condence interval contains 50% O B. Yes. it is a plausible claim because the condence interval does not contain 50% O C. No, it. is not a plausible claim because the condence interval does not contain valu above 50%. O D. Yes. it is a plausible claim because the condence interval contains values above 50%. The accompanying histogram shows the number of runs scored by baseball teams for three seasons. The distribution is roughly unimodal and symmetric, with a mean of 687 and a standard deviation of 69 runs. An interval one standard deviation above and below the mean is marked on the histogram. Complete parts (a) through (c) below. Click the icon to view the histogram. a. According to the Empirical Rule, approximately what percent of the data should fall in the interval from 618 to 756 (that is, one standard deviation above and below the mean)? Approximately |% of the data should fall in the interval from 618 to 756. b. Use the histogram to estimate the actual percent of teams that fall in this interval. How did your estimate compare to the value predicted by the Empirical Rule? O A. 69% of the data falls in the interval from 618 to 756. The estimate is not close to the value predicted by the Empirical Rule. O B. 94% of the data falls in the interval from 618 to 756. The estimate is very close to the value predicted by the Empirical Rule. O C. 50% of the data falls in the interval from 618 to 756. The estimate is not close to the value predicted by the Empirical Rule. O D. 69% of the data falls in the interval from 618 to 756. The estimate is very close to the value predicted by the Empirical Rule. c. Between what two values would you expect to find about 95% of the teams? You expect to find about 95% of the teams between the two values ] and . Simplify your answers. Use ascending order.)