Answered step by step
Verified Expert Solution
Question
1 Approved Answer
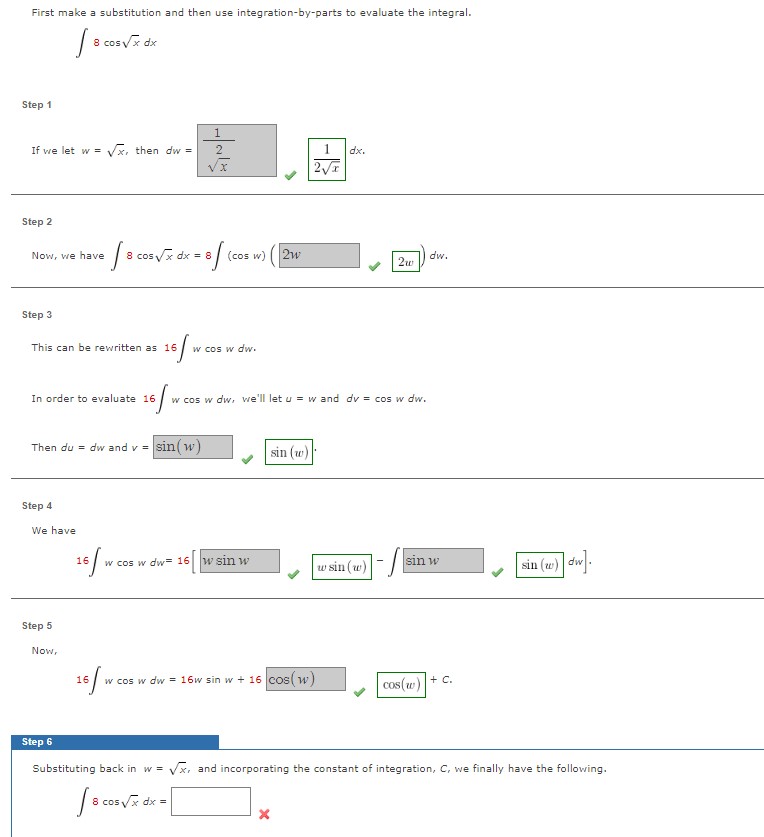
First make a substitution and then use integration - by - parts to evaluate the integral. 8 c o s x 2 d x Step
First make a substitution and then use integrationbyparts to evaluate the integral.
Step
If we let then
Step
Now, we have
Step
This can be rewritten as wcoswdw.
In order to evaluate wcoswdw, we'll let and
Then and
Step
We have
wcoswdw
Step
Now,
wcoswdwwsinw
Step
Substituting back in and incorporating the constant of integration, we finally have the following.
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


