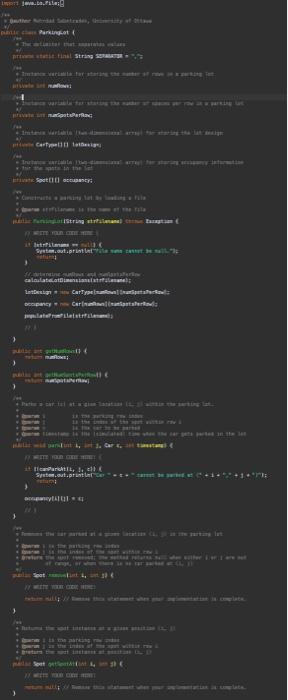
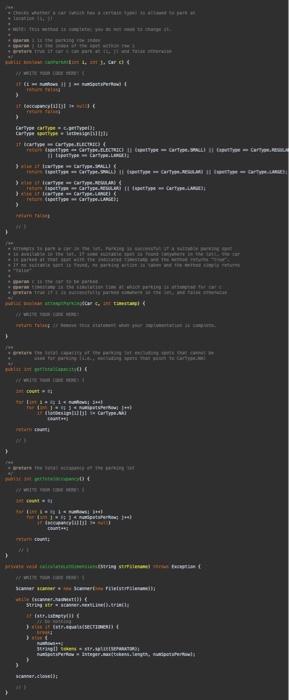
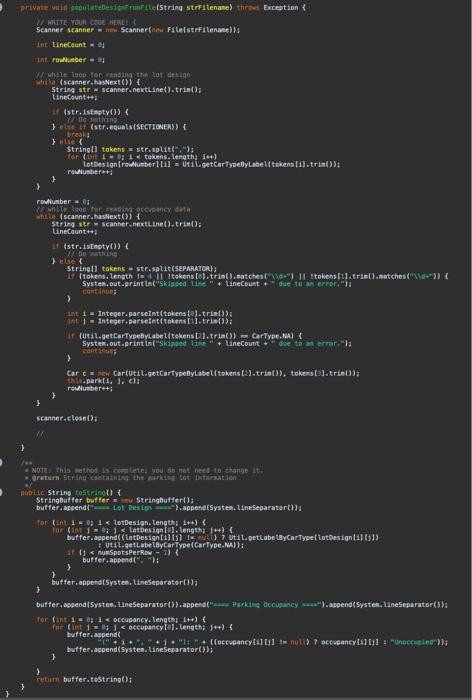
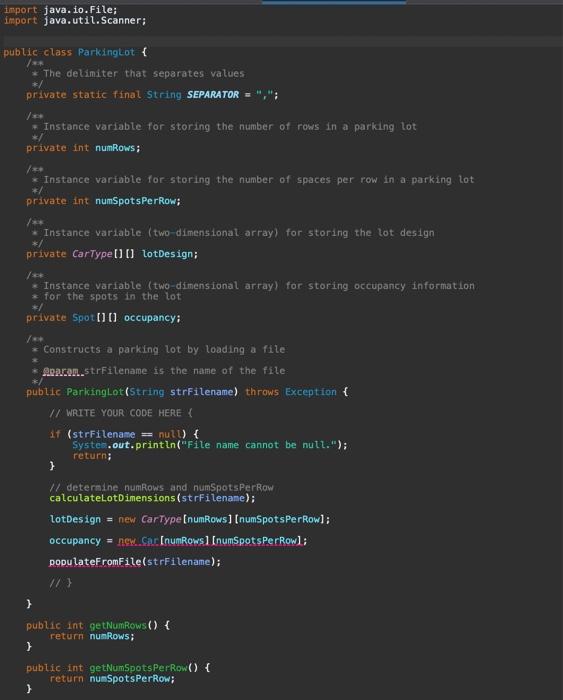
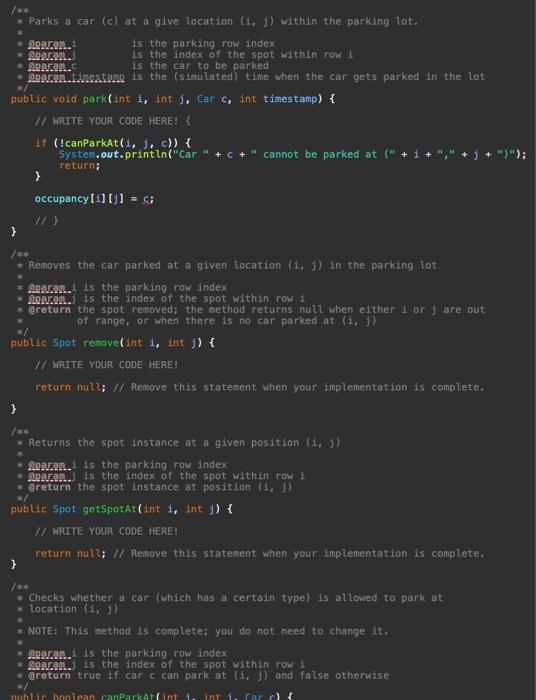
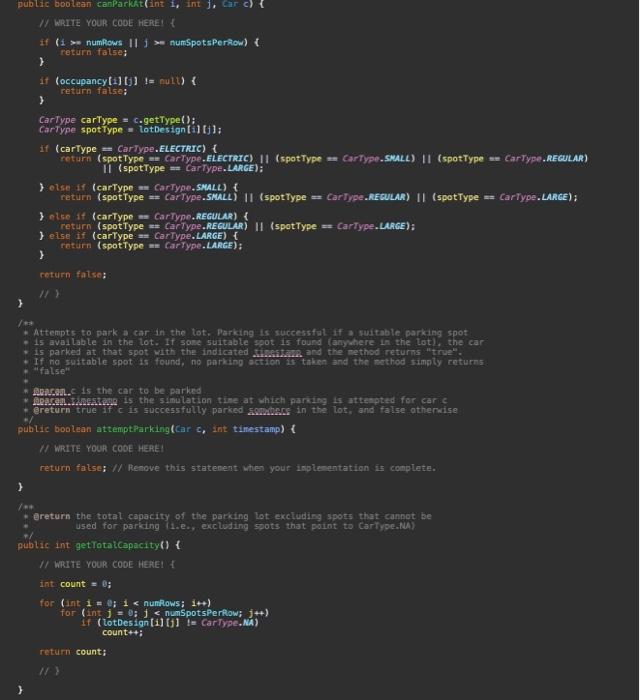
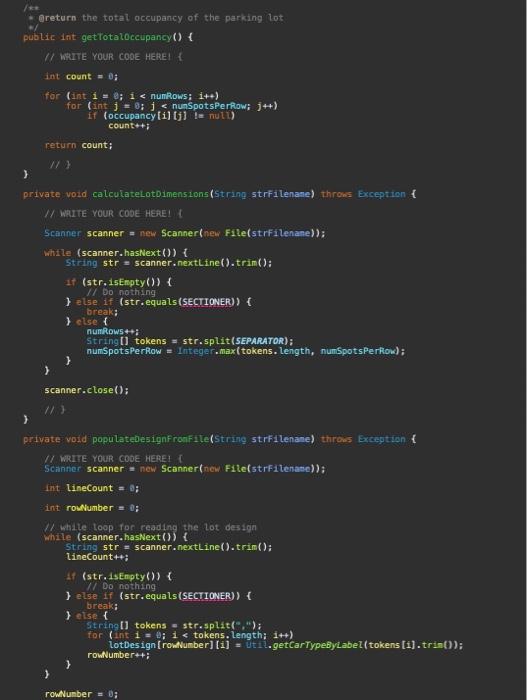
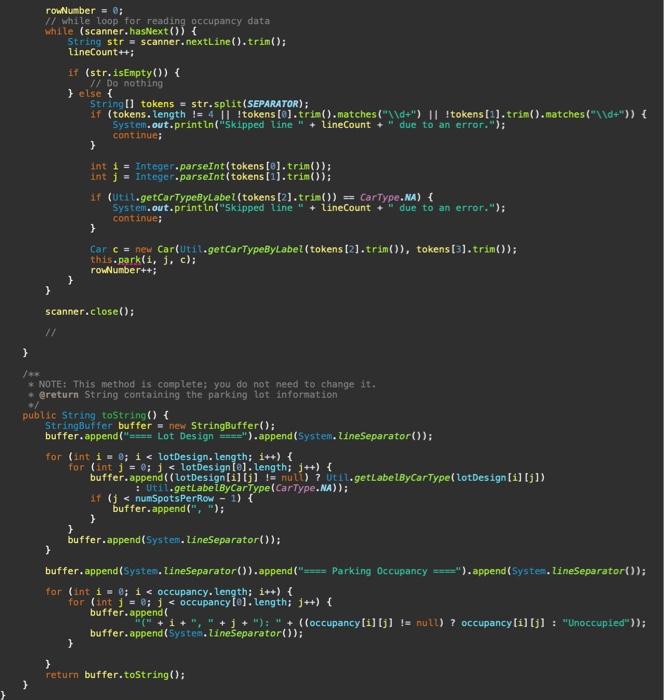
fix the following above code according to the instructions below:

1 (isting (i) 3 13 1 1 1 3) int Hineceunt =1 int rowataber: =14 (f whlle toop. for readaga the lot aes igin. While (scacher, hassext (b) 1 String ste o scanner. nextline(3, trint\} linecount+4i if (str,istasty(\}) \& 1. stie if (str.eguats(sectrouen) if bitisest Stringl] tokens = strisplit (i)1 3 rowisuber =03 mile (scanner. haskext ($) i String ste = seanner, nextcine (3,tri=[1; tineCaunt tot if (str.1stnsty()) i H exte f 5trinell tokens i strisplit (SEPARATCQ); 3 Mant 1 = Inteperi parseint ( tokens to1 t trint ) ) thisparkin 1,1 . cla 3 seanner-closed)i: 4 nubtic strine tostrieg( ) Stringbuffer bufter = szy Stringhuffer(); butfer aspend 1 3 Task 3. Complete / revise the ParkingLot class. For this task, you will mostly reuse what you did in Al yourself or alternatively build on the Al reference solution provided to you. There are a number of important differences between Parkinglot in Al and Parkinglot in A2 : - Occupancy is no longer tracked using a two-dimensional array of cars. Instead, a two-dimensional array of Spots is used, so that we can record when each car was parked in the lot. This change necessitates a number of minor enhancements to the methods that you implemented previously in ParkingLot. - The input file to be processed by the constructor of Parkinglot no longer contains any occupancy informatisn. In A2, the input file contains only the parking-lot design information. We will see in Tasks 4 where the cars that want to park in the lot are coming from. In A2, you will no longer read the occupancy information from a file. - You will implement a new method public boolean attemptParking(Car c, int tinestamp). This method, which will be used for the implementation of Task 4, checks whether there is any suitable spot in the lot for car c based on c's type and the car-type restrictions that need to be observed (e.g., large cars being allowed to park only in large spots). The car-type restrictions are exactly as defined in Al. If a suitable spot is found, the following happens: (1) c is parked in the lot and the associated timestamp is set to the times tanp parameter of at temptParkingl....); (2) the method call will return true. 1. Set the simulation clock ta zero; If this clock counts in seconds (s) 2. Repeat until the simulation clock has reached 24h(i.e.24+3600s)1 3. Probabilistically determine whether a car arrives this very second (yes ( no): 4. If a car arrives this second, generate a randion car and place it in the inconing queue: 5. Far every car c parked in the lat \{ 6. Calculate the duration that c has been parked; 7. If (duration ==8h ) remove the car from the lot and place it in the butgoing queue: Else (i.e., when duration \& Bh) \{ 9. Protabilistically determine whether c leaves this very second (yes o ): 10. If c is leaving, remave the car fron the lot and put in the outgaing queue; 11. 12. 13. If the incoming queue is not empty, attempt to park the first car fran the this queue; 14. If the autgaing queue is not empty, let the first car in this quece aut; 15. Increase the sinulation clock by 15 ; 16. 1 Iigure 3: The simulation algorithm (pseudo-code) that the parking lot does not currently have a suitable spot to accommodate c. This in turn means that c has to wait until a suitable spot becomes available, i.e., until a currently parked car leaves and the vacated spot is able to accommodate c based on its type. For example, if c is of type LARGE, it has to wait until a LARGE spot becomes vacant before c is aliowed into the lot