Question: For ER and s> 0, define 0 (x):= e-||||1/s, where ||||1= |x| ++ |n| is the norm of a. For a lattice LCR, parameters

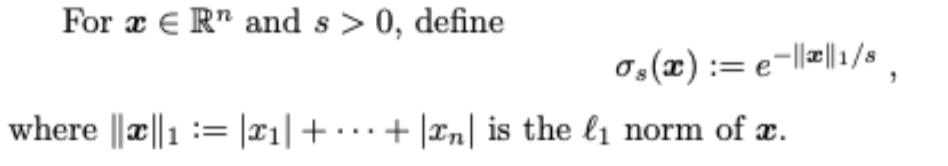
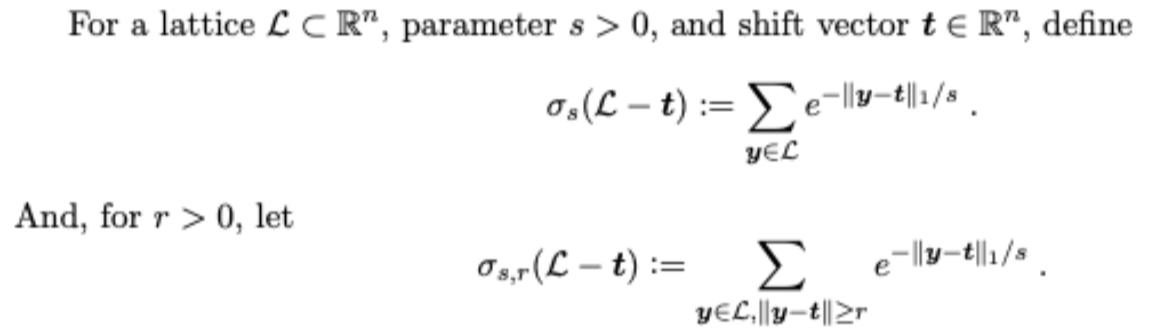
For ER and s> 0, define 0 (x):= e-||||1/s, where ||||1= |x|

++ |n| is the norm of a. For a lattice LCR", parameters

> 0, and shift vector t ER", define Os (L-t) := e-||-t||1/s

For ER and s> 0, define 0 (x):= e-||||1/s, where ||||1= |x| ++ |n| is the norm of a. For a lattice LCR", parameters > 0, and shift vector t ER", define Os (L-t) := e-||-t||1/s YEL And, for r> 0, let Os,r (Lt):= e-ly-t||1/s YEL,|y-t||zr Prove that for any lattice LCR", tER", parameter s > 0, and r > ns, Osr (L-t) (er/(ns))".e-/s.o(L).

Step by Step Solution

★★★★★

3.46 Rating (166 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

It looks like the function fx is defined as fx exs ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Accounting Questions!

The norm of a linear transformation TA: Rn Rn can be defined by where the maximum is taken over all nonzero x in Rn. (The subscript indicates that the norm of the linear transformation on the left is...

Define L : (0, ) R by a) Prove that L is differentiable and strictly increasing on (0, ), with L'(x) = 1/x and L(l) = 0. b) Prove that L(x) as x and L(x) - as x 0+. (You may wish to prove for...

Let X be a binomial random variable with parameters n and p. Show that p)n+ n + Dp

What are the three elements of Juran's Trilogy? Question Planning, Six Sigma, and Control Planning, Improvement, and Control Planning Six Sigma and Inspection Planning, Improvement, and Inspection

All other things being equal, the numerical difference between a present and a future value corresponds to the amount of interest earned during the deposit or investment period. Each line on the...

Part 4: Test your code: Use the following code to test your results. Copy the output and turn in as PDF. public class TestList { static final int N = 4; public static void main(String[] args) {...

Give the typing rules for Peano natural numbers and their eliminator.(ii) Using the rules given above, define the addition function.] (iii) Let a binary tree be either a leaf Leaf or a node...

1 Write three Scheme procedures to simulate these three gates: AND, OR, and NOT, shown in the diagram in Figure 1. Test your procedures using all possible input combinations. Hint: Lecture slides...

*****Scheme is the coding language used, specifically in Dr. Racket****************** 1 Write three Scheme procedures to simulate these three gates: AND, OR, and XOR, shown in the diagram in Figure...

Finish the code to match the guidelines: #include #include //provides definitions for using PLplot library #include #include #define NUM_POINTS 500 #define X_IX 0 #define FX_IX 1 #define TRUE 1...

a. The accounts receivable confirmation work revealed one pricing misstatement. The book value of $12,955.68 should be $11,984.00. The total misstatement based on this difference is $14,465, which...

Two teenagers, Iain and Kay decide to play Chicken. They approach each other in sports cars from opposite directions at high speed. At the point where they are very close they must simultaneously...

What does "random walk" refer to in the context of the stock market? Option A A continuous upward trend in stock prices. Option B The theory that future prices cannot be predicted based on past...

Calculate the missing values in problem. Assume in each case that the payment is made within the discount period. Invoice Amount credited amount ($) Credit terms Payment ($) ($) Balance owed ($)...

A concrete pile 20 m long having a cross section of 0.46 m 0.46 m is fully embedded in a saturated clay layer. For the clay, given: sat = 18 kN/m 3 , = 0, and c u = 80 kN/m 2 . Determine the...

Blood pressure is measured with a sphygmomanometer while the sound from the pulse is checked. Investigate how this works, list the range of pressures normally recorded as the systolic (high) and...

Are preferred shares automatically nonvoting?

An elderly woman has been having trouble caring for herself in her own home. Twice now, in the middle of the night, she has called an ambulance and has been taken to the hospital for chest pains....

What value best represents the score at the first quartile(Q1)

Find the least squares straight line fit to the three points (0, 0), (1, 2), and (2, 7).

Let C3 have the Euclidean inner product. Else the Gram-Schmidt process to transform the basis (u1, u2, u3) into an orthonormal basis. u1 = (i, i, i), u2 = (- i, i, 0), u3 = (i, 2i, i)

Let T: R3 V be a linear transformation from R3 to any vector space. Show that the kernel of T is a line through the origin, a plane through the origin, the origin only, or all of R3.

Table 20P-4 shows an economys GDP, current expenditures, and tax revenue for 20132016. a. Complete the table by filling in the prior-year debt for each year listed. b. For each year, is this economy...

For each of the scenarios below, determine whether you think it is likely that an employer could be discriminating against a person because of his or her age. Explain why or why not. a. A young...

Some economists have studied the effects of lookism, or discrimination based on how attractive a person is. Give an example of a case in which the market might encourage lookism and an example of a...