For this assignment you are to create a menu based mathematical tool. Your menu should provide the user with three options: 1. Calculate the area under a curve, 2. Calculate the slope of a curve between two points, or 3. Exit.

Your program should loop through the menu and perform the requested operations until the user selects the exit option (choice #3). If the user selects an invalid menu option the program should notify the user of this error and then prompt for a new user entry.The equation of the curve that your program will evaluate is a polynomial of the form(where any of the coefficients: a, b, c, d, or e can be zero):

After the user selects option 1 or 2 (i.e., area under curve or slope between two points), the user should be prompted to specify the coefficients (a, b, c, etc.) of the curve. This will be the equation used in the calculation.

Menu Option #1(Area under the curve) If this menu option is selected, the user should be prompted for xmin, xmax and the number of rectangles used in the calculation. The final result should be printed to the screen, along with the actual solution obtained via integration of Equation 1.To approximate the area under the curve, in the interval from xmin to xmax, one can calculate the area of a series of rectangles that fit under that curve (see Figure 1) from xmin to xmax. For example, the figure below, the height of a rectangle is equal to the value of the function at the left edge of that rectangle.

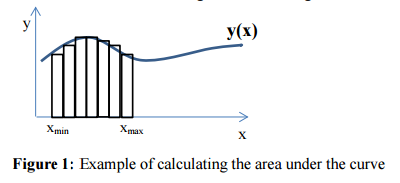
Menu Option #2(Slope between two points) For this option, the user should be prompted for the two x values (x1 and x2) that are to be used in the calculation of the slope of the curve between these two x values. The slope between two points is calculated by taking the difference in y divided by the difference in x (see Figure 2). The final result should be printed to thescreen, along with the actual solution obtained via differentiation of Equation 1.

Menu Option #3 (Exit)If the user selects option 3, the loop will exit and the program will finish.

y(x) Xmin Xmax Figure 1: Example of calculating the area under the curve