For this assignment, you are to write a program to multiply two sparse matrices. You will implement a data structure that facilitates efficient processing of sparse matrices so that your program will process rather large matrices quickly.

Functional Requirements

The user requires a program that will read two input files, each describing a matrix, and produce an output file describing the product of the two matrices. This section describes how two matrices are multiplied and how the input and output files are structured.

Matrix multiplication

A matrix is a 2-dimensional array of numbers, but for the purposes of this assignment, it is best thought of as a 1-dimensional array of vectors, each of which is a sequence of numbers. For example, the following is a 2x3 matrix:

A=(2341.502)

We can view it as either a 2-element array containing the row vectors (2, 3, -4) and (-1.5, 0, 2) or a 3-element array containing the column vectors (2, -1.5), (3, 0), and (-4, 2).

Suppose we want to multiply two matrices A and B. To define this product, it is best to think of A as an array of row vectors and B as an array of column vectors. The product AB will have the same number of rows as A and the same number of columns as B. Each element of AB is defined using a vector operation known as a dot product. Let u and v be two vectors having the same number of elements:

u = (u1, . . . um)

v = (v1, . . . vm)

Then the dot product of u and v is defined to be the following:

u1v1 + . . . + umvm

For example, the dot product of (2, 3, -4) and (-1, 0 -2) is:

2x(-1) + 3x0 + (-4)x(-2) = -2 + 0 + 8 = 6

Ordinarily, the definition of a dot product requires that the two vectors have the same number of elements. However, we can extend this definition to two vectors of different lengths by ignoring the extra elements at the end of the longer vector.

We can now return to the definition of the product of two matrices A and B. The element in row i and column j of the product AB is defined to be the dot product of the vector in row i of A with the vector in column j of B. For example, suppose we want to compute the product of the 2x3 matrix A shown above and the following 3x4 matrix:

B=(102103012000)

To compute the value in row 0 and column 0 of the result, we find the dot product of row 0 of A (i.e., (2, 3, -4)) and column 0 of B (i.e., (-1, 0, -2)). As we saw above, this dot product is 6. Likewise, the value in row 0 and column 1 is the dot product of (2, 3, -4) and (0, -3, 0), or -9. The full 2x4 product is the following:

AB=(69412.5031.5)

Ordinarily, we would require the number of columns in A to be the same as the number of rows in B. However, because we have relaxed the definition of a dot product so that it applies to vectors of different lengths, the definition we have given for matrix multiplication makes sense for any two matrices. For example let C = AB as computed above. Then

CA=(69412.5031.5)(2341.502)=(62+(9)(1.5)63+(9)06(4)+(9)2(2.5)2+0(1.5)(2.5)3+00(2.5)(4)+02)=(25.5184257.510)

Note that the extra elements in each row of C are simply ignored.

File format

The matrices that the user needs to multiply are sparse; i.e., while they may contain a large number of elements, most of them are 0. For example, a 1000x1000 matrix contains a million elements; however, if it is sparse, all but maybe a few thousand of them will be 0. The file format used will take advantage of this sparseness in order to keep file sizes small.

The input and output files will be plain text files. Each line of the file will contain a sequence of numbers separated by commas. An mxn matrix will be described as follows:

The first line will give the number of rows (m) and the number of columns (n). Both of these values are integers.

Each nonzero entry in the matrix will be described by a line of the file. This line will contain:

the row number of the entry (a nonnegative integer less than m),

the column number of the entry (a nonnegative integer less than n), and

the entry itself (a floating-point number).

For example, consider the following input file:

2,3 0,0,2 0,1,3 0,2,-4 1,0,-1.5 1,2,2 

This file encodes the 2x3 matrix A given above. The lines of this file indicate the following:

Line 1: The matrix has 2 rows and 3 columns.

Line 2: The element in row 0 and column 0 has a value of 2.

Line 3: The element in row 0 and column 1 has a value of 3.

etc.

Note that the 0 entries in the matrix are not encoded explicitly - any entry that is not described by an input line (such as row 1, column 1 in TestA.csv) is assumed to be 0. Note also that the nonzero elements can be listed in any order; however, we expect that in most cases, they will be given either by rows from top to bottom, and left to right within each row, or by columns from left to right, and from top to bottom within each column. Output files should be produced in the former order (i.e., by rows).

Starting the Assignment

Create a GitHub repository using this URL (Links to an external site.)Links to an external site., and clone it to your local machine. This solution contains a new Windows Forms Application in which Form1.cs has been renamed UserInterface.cs. Also included are a sample executable hw2.exe and a folder called Data containing some test files.

User Interface

We need to be able to obtain the locations of two input files and one output file from the user, and once these file locations have been obtained, to compute the matrix product. Therefore, a GUI resembling the following should be used:

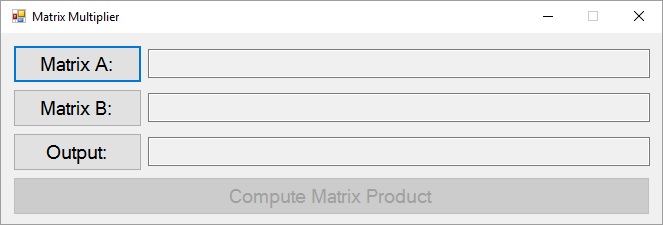
Each of the three TextBoxes should be read-only (using their ReadOnly properties), and the "Compute Matrix Product" button should be initially disabled. Furthermore, it should be impossible to maximize or otherwise resize this window (this can be done by setting the Form's MaximizeBox property to false and its FormBorderStyle property to Fixed3D).

The three smaller buttons will be used to obtain file locations from the user. Thus, if the user clicks either the "Matrix A:" button or the "Matrix B:" button, an OpenFileDialogshould be displayed, or if the user clicks the "Output:" button, a SaveFileDialog should be displayed. For each of these dialogs, there should be no file name initially displayed, although a file name may be displayed when the dialog is subsequently opened. Furthermore, each file dialog should have a filter which initially causes only files with a suffix of ".csv" to be displayed, but may be changed by the user to display all files.

If the user selects a file from any of these dialogs, the full path name of the file selected should be displayed in the TextBox next to the button that was clicked (if the name doesn't fit, you should be able to click on the TextBox and scroll it left or right using the arrow keys). If the user closes the dialog without selecting a file, the content of the TextBoxes should remain unchanged. When all three TextBoxes are nonempty, the "Compute Matrix Product" button should be enabled and remain enabled for the remainder of the program's execution. Note that the files may be selected in any order, and that once a file is selected, it may be changed at any time by clicking the corresponding button.

If the "Compute Matrix Product" button is clicked, the program should attempt to read a matrix A from the file named in the TextBox next to the "Matrix A:" button, and to read a matrix B from the file named in the TextBox next to the "Matrix B:" button. It should then attempt to write the product AB to the file named in the TextBox next to the "Output:" button using the same file format. Once the product matrix has been successfully written, it should display a MessageBox containing the message, "Matrix written."

Exception handling

Your program does not need to verify that the input files conform to the format described above. However, if it contains two (possibly identical) nonzero values for the same matrix location, it should display within a MessageBox an InvalidOperationException containing the message, "Attempt to add a value at an index that already has a value." Furthermore, if incorrect file formats or other I/O issues lead to an exception being thrown, the exception should be displayed in a MessageBox. Whenever an exception is displayed, all processing of the current input files should stop.

Software Architecture

You will need to define two classes, along with the UserInterface class and the LinkedListCell class from Lab Assignments 10-12 and 14, as shown in the following class diagram:

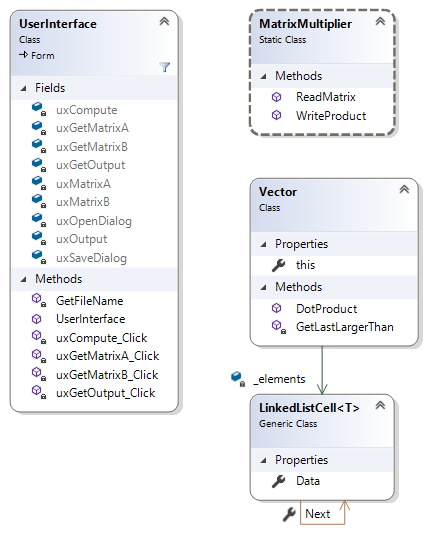
MatrixMultiplier is a static class containing methods needed for I/O and multiplying two matrices. Instances of the Vector class will represent rows or columns of a matrix. The arrow from the Vector class to the LinkedListCell class indicates that the Vector class includes a field of type LinkedListCell for some type T. The arrow from LinkedListCell back to itself indicates that its Next property accesses another instance of this class.

Coding Requirements

Specific requirements for the above classes are given in what follows. Feel free to add other private methods if you feel it improves the code. Don't add any more publicmembers.

The LinkedListCell Class

To incorporate this class into your code, copy the file LinkedListCell.cs from a solution to one of Lab Assignments 10-12 or 14 to the folder containing the source code for this assignment. Then in the Visual Studio Solution Explorer, right-click on the project name (below the solution name) and select "Add->Existing item...". In the resulting file browser, select LinkedListCell.cs. This file should then appear in your Solution Explorer. You will then need either to change the namespace in this file to match the namespace for the rest of your program, or add a using directive for this namespace to your Vectorclass file.

The Vector Class

This class should be public and non-generic (i.e., it should not have a type parameter). It should implement a vector with arbitrary integer indices. Its design will be particularly appropriate for sparse vectors, as it will only store nonzero entries explicitly. The nonzero entries will be stored in a linked list of KeyValuePair (Links to an external site.)Links to an external site.s.

In order to facilitate building a vector efficiently when elements are added in order of increasing index, these elements should be stored in decreasing order of index (i.e., from largest index to smallest index). In order to facilitate easier updates, the linked list should begin with a header cell, as in Lab Assignment 14. While its Data property will be ignored by your code, you should treat it as though the index it stores is larger than any other index. You will need a private field to store a reference to the linked list - you can just initialize this field to a new cell, which will be the header cell.

For example, the vector (2, 0, -1, 0, 0, 0, 3) would be represented by the following linked list:

This class will need three other members, which are described in what follows.

A private method to find the last cell with an index greater than a given index

This method should take as its only parameter an int giving an index into the vector. It should return a LinkedListCell> referring to the last cell in the list (given by the private field) whose index is greater than the given index. You should assume that the header cell has an index larger than any index in the list (though you shouldn't look at the data in the header cell).

A public indexer to add a value at an index

An indexer's definition (Links to an external site.)Links to an external site. is similar to a property definition, in that it may include a getand/or a set accessor. This indexer will need only a set accessor in order to allow user code to modify the vector's components (user code will not need to retrieve individual components). You will need to use the most general form in which a block of code is included in the accessor:

 public double this[int i] { set { // Code to set the value at index i } } 

Note that the name of an indexer is always this. The code will need to use the above method to find the last cell whose index is greater than i. If the following cell contains an equal index, it should throw an InvalidOperationException containing the message specified under "Exception handling" above. Otherwise, it should insert a new KeyValuePair containing the given index and value (the value can be obtained from the keyword value, which contains the value the user code is assigning to index i).

A public method to compute a dot product

This method should be static (Links to an external site.)Links to an external site.. It should take two Vectors as its parameters and return a double. Because the method is static, you will not have access to the (non-static) private field; however, you will be able to access this field as a member of each of the parameters. This method will therefore process two linked lists, one taken from each of the given Vectors. You will need a variable to accumulate a sum, as well as two variables, one for each list, to walk through the lists together; they can each start at the cell following the header cell. The sum will need to include the products of all pairs of values that are at the same index in the two lists - all other values will be multiplied by 0, and hence contribute nothing to the sum. Because the lists are ordered by decreasing index, you will need just one loop that iterates as long as both of the variables walking through the lists are non-null. On each iteration, if the keys in the two cells are equal, add the product of their values to your sum, and advance both variables; otherwise, advance the variable referring to the larger index, as this index cannot occur in the other list. Once the loop has completed, return the sum.

The MatrixMultiplier Class

This class must be public and static. It will need two public static methods.

A method to read a matrix

This method will be responsible for reading a matrix and forming an array of either row vectors or column vectors from it. It needs to return a Vector[ ], but some of the parameters need some explanation. One of the parameters needs to be a string giving the name of the file to be read. The remaining parameters will control whether it builds an array of column vectors or of row vectors. We can think of the input lines as consisting of 2 or 3 fields, depending on whether the line is the first in the file. Field 0 will correspond to rows (i.e., it will be either the number of rows or a row index), and field 1 will correspond to columns. If we are building an array of row vectors, the array indices will come from field 0, and the indices into the Vectors will come from field 1. Conversely if we are building an array of column vectors, the array indices will come from field 1, and the indices into the Vectors will come from field 0. Thus, in order to be able to specify which type of array we are building, we need two int parameters - one to specify which field will be used for array indices, and another to specify which field will be used for indices into the Vectors.

This method will need a StreamReader (defined within a using statement) to read from the given file. It should read the input a line at a time. Each of these lines will be read as a string. To split one of these strings into fields, use its Split (Links to an external site.)Links to an external site. method, passing ',' as its only parameter. This method will return a string[ ] whose elements are the different fields of the line. You can then convert these strings to the appropriate type using either Convert.ToInt32 (Links to an external site.)Links to an external site. or Convert.ToDouble (Links to an external site.)Links to an external site.. The first line will need to be handled separately. Based on the values on this line, you can construct an appropriately-sized array of Vectors. Note that each of these array elements will be automatically initialized to null - in order to get any Vectors, you will need to iterate through the array and initialize each element to a new Vector. To fill these Vectors, you will need a loop that reads the remaining lines of the file and adds each value read from field 2 to the appropriate location of the appropriate Vector. Note that because of the way you defined a Vector's indexer, you can index into it like you would an array.

A method to compute a matrix product

This method will take as its parameters two Vector[ ]s giving the matrices to multiply and a string giving the name of the output file. It should return nothing. You will need a StreamWriter (Links to an external site.)Links to an external site., defined within a using statement, for writing to the output file. You may assume that the first Vector[ ] parameter is an array of row vectors, and that the second is an array of column vectors. Using the sizes of these arrays, you can determine the number of rows and columns of the output matrix, which you will need to write to the first line of output, separated by a comma. Then set up nested loops that iterate through the rows and columns of the product matrix. For each pair of indices, compute the element at that location using the method to compute a dot product (from the Vector class), and if it is nonzero, write it to the output file following the format specified above. (Don't try to store the product matrix - just write it out as you compute it.)

The UserInterface Class

You will need an event handler for each of the four buttons, plus one other private method.

A method to get a file name from the user

This method should take a TextBox and a FileDialog (Links to an external site.)Links to an external site. as its parameters and return nothing. FileDialog is a super-type of both OpenFileDialog and SaveFileDialog; hence, either of these types may be passed as this parameter, and it may be used in a similar way as either of these types. This method is responsible for showing the given FileDialog to the user, and if the user selects a file, placing the file name in the given TextBox. If this causes all three TextBoxes to be nonempty (i.e., to contain nonempty strings), it should enable the "Compute Matrix Product" button.

Event handlers

Given the methods above, your event handlers should be straightforward. You should do your exception handling within the event handler for the "Compute Matrix Product" button. Note that the other three buttons should only update the GUI - they should not result in any file I/O.

Testing Your Program

The GithHub repository contains several input files for you to use to test your program:

TestA.csv: the 2x3 matrix shown under "Mathematical Background" above

TestB.csv: the 3x4 matrix shown under "Mathematical Background" above

TestC.csv: a 2x4 matrix with invalid row numbers

TestD.csv: a 3x4 matrix with one element repeated

bcsstk08.csv: a 1075x1075 matrix with 7017 nonzero elements

bcsstk09.csv: a 1084x1084 matrix with 9760 nonzero elements

bfw782a.csv: a 783x783 matrix with 7514 nonzero elements

illc1033.csv: a 1034x321 matrix with 4732 nonzero elements

illc1850.csv: a 1851x713 matrix with 8758 nonzero elements

random.csv: the above matrix with elements listed in random order

The last six of these matrices are derived from matrices downloaded from Matrix Market (Links to an external site.)Links to an external site. of the National Institute of Standards and Technology (NIST) (Links to an external site.)Links to an external site..

Your program should be able to multiply any two of the above in either order, or any one of them by itself, except TestC.csv and TestD.csv. TestC.csv should throw an exception when used as matrix A (but not as matrix B), and TestD.csv should always throw an InvalidOperationException with the message, "Attempt to add a value at an index that already has a value." You should also be able to use output files produced by your program as input files, though the performance may be degraded due to more nonzero entries in the matrices. The files produced by your program should be identical to the files produced by the executable provided. You can compare two files with the Windows command, comp. You can run this command by holding down the "Windows" key while typing "R", then typing "comp" (without the quotes) in the resulting dialog. If you've saved your output files to your Desktop, then you can specify the files to the comp program using the form "Desktop\filename.csv".

Performance

The performance should be comparable (within a factor of 2) to that of the posted executable on all of the input files provided. A good test of performance is to multiply bcsstk08.csv by itself, then multiply the result by itself.

Submitting Your Assignment

Be sure to refresh your Team Explorer, commit all your changes, then push your commits to your GitHub repository. Then submit the entire URL of the commit that you want graded. There is no need to submit a comment, as you will not have a completion code.

Important: If the URL you submit does not contain the 40-hex-digit fingerprint of the commit you want graded, you will receive a 0, as this fingerprint is the only way we can verify that you completed your code prior to submitting your assignment. We will only grade the source code that is included in the commit that you submit. Therefore, be sure that the commit on GitHub contains all six ".cs" files, and that they are the version you want graded. This is especially important if you had any trouble committing or pushing your code.

A Note on

A=(-1.5 24) 3 1.5 02 A=(-1.5 24) 3 1.5 02