For this problem, I have to plot the unit step response of a second order system in Matlab. I have been working on the code for the problem with all the provided information, but I am not sure how the professor expects me to use IF statements and FOR and WHILE loops in my code.
For this activity, we are going to explore the response of a classic second order system to a unit step input. A unit step input is similar to something we covered something in class for some period of time it is off, then it is on (and stays on this is different from the square wave)

The following is the expectations for this program...

This is my code, it runs but it doesn't plot anything please help!
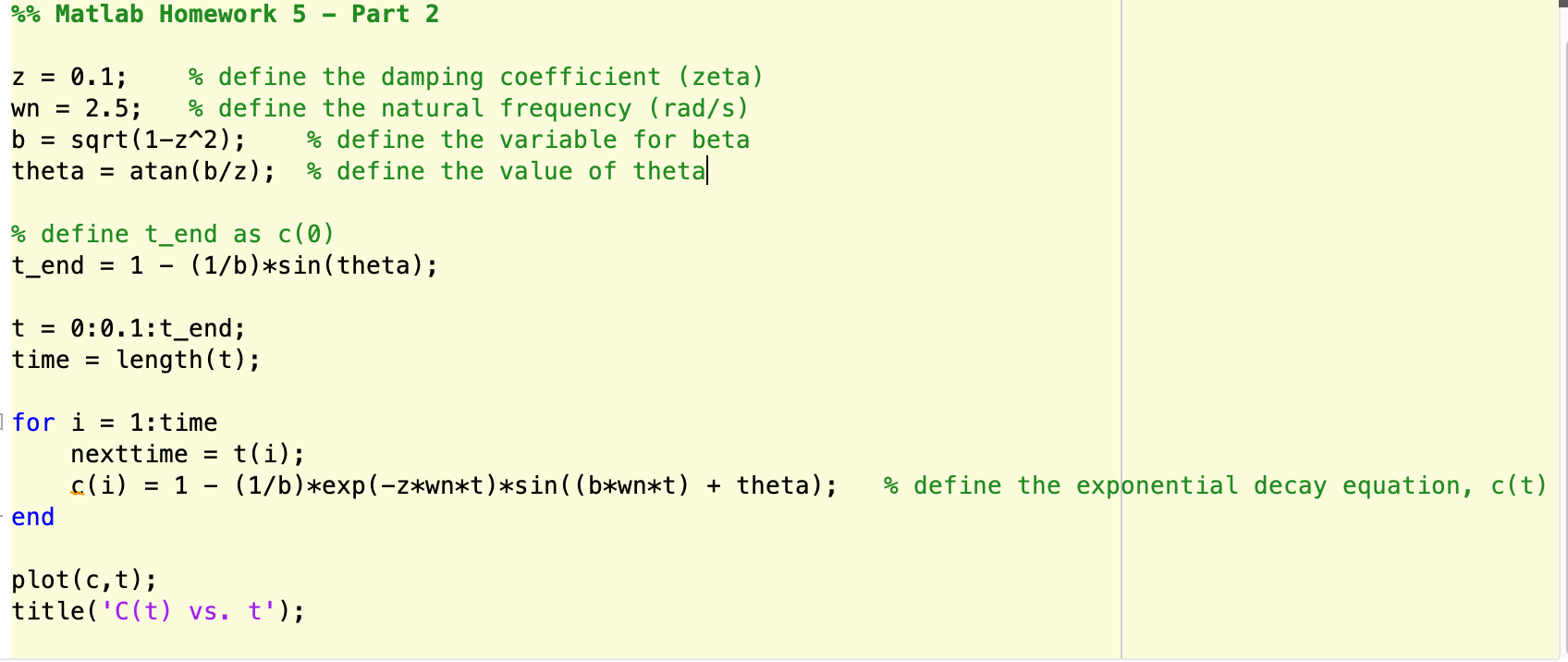
The response of the system (c(t)) can be modeled using the following relation ... 1. - omt. c(t) = 1 -=*e-Swnt * sin(wnt + 0) B B = V1 32 tan(0) = B =beta = zeta on = natural frequency o = theta Oooh! Exponential decay - when does it "reach the end? Before we get too far in to it .... Note that this is an exponential decay coupled with a sinusoid - you should be able to visualize/predict the type of responses that you will see from this function. This may look complicated - but think about what you are given and what you want to solve for in the assignment. It is no more difficult to plot than the projectile motion project. Create a single plot of the unit-step response of this second-order system by calculating and plotting c(t) vs. t for the following parameters ... o Damping coefficient (C) = 0.1 o Natural frequency (on) = 2.5 rad/s Explore the plot before "finishing with this section - be certain to adjust the length of the time vector to accurately capture the complete response of the system Use comments in your code to describe what you have observed. For this project you may only use IF statements and FOR or WHILE loops. You may not use the function called STEP" (a specialized MATLAB built-in routine) for solving this problem. %% Matlab Homework 5 - Part 2 z = 0.1; % define the damping coefficient (zeta) wn = 2.5; % define the natural frequency (rad/s) b = sqrt(1-z^2); % define the variable for beta theta = atan(b/z); % define the value of theta % define t_end as c(0) t_end = 1 - (1/b)*sin(theta); t = 0:0.1:t_end; time = length(t); for i = 1:time nexttime = t(i); c(i) = 1 - (1/b)*exp(-z*wn*t)*sin((b*wn*t) + theta); - end % define the exponential decay equation, c(t) plot(c,t); title('C(t) vs. t'); The response of the system (c(t)) can be modeled using the following relation ... 1. - omt. c(t) = 1 -=*e-Swnt * sin(wnt + 0) B B = V1 32 tan(0) = B =beta = zeta on = natural frequency o = theta Oooh! Exponential decay - when does it "reach the end? Before we get too far in to it .... Note that this is an exponential decay coupled with a sinusoid - you should be able to visualize/predict the type of responses that you will see from this function. This may look complicated - but think about what you are given and what you want to solve for in the assignment. It is no more difficult to plot than the projectile motion project. Create a single plot of the unit-step response of this second-order system by calculating and plotting c(t) vs. t for the following parameters ... o Damping coefficient (C) = 0.1 o Natural frequency (on) = 2.5 rad/s Explore the plot before "finishing with this section - be certain to adjust the length of the time vector to accurately capture the complete response of the system Use comments in your code to describe what you have observed. For this project you may only use IF statements and FOR or WHILE loops. You may not use the function called STEP" (a specialized MATLAB built-in routine) for solving this problem. %% Matlab Homework 5 - Part 2 z = 0.1; % define the damping coefficient (zeta) wn = 2.5; % define the natural frequency (rad/s) b = sqrt(1-z^2); % define the variable for beta theta = atan(b/z); % define the value of theta % define t_end as c(0) t_end = 1 - (1/b)*sin(theta); t = 0:0.1:t_end; time = length(t); for i = 1:time nexttime = t(i); c(i) = 1 - (1/b)*exp(-z*wn*t)*sin((b*wn*t) + theta); - end % define the exponential decay equation, c(t) plot(c,t); title('C(t) vs. t')









