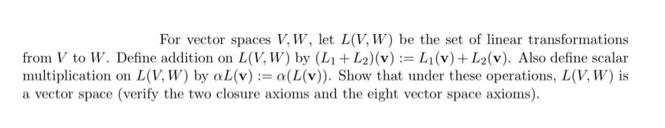
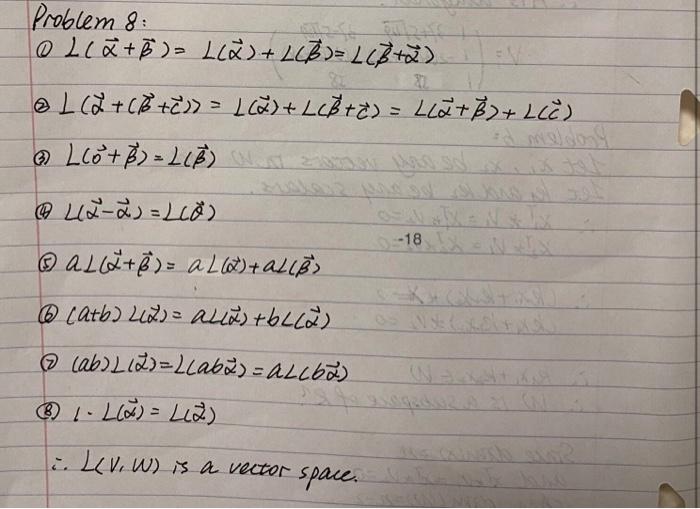
For vector spaces V, W, let L(V, W) be the set of linear transformations from V to W. Define addition on L(V, W) by (L1+ L2)(v) := L1(v)+ L2(v). Also define scalar multiplication on L(V, W) by aL(v) := a(L(v)). Show that under these operations, L(V, W) is a vector space (verify the two closure axioms and the eight vector space axioms). Problem 8: 0 lc&+B)= Ll)+LB=L+) eL(+C+>=1)+L8+)= Lla+B)+ Li) @ Lo+B) = LLB) -18 NN 1080 cab)LI2)=2Laba) = aLLbd) likkliw)is a vector . space.