From the text answer questions 1 and 2. Let G = (V, E) be an undirected graph with n nodes. Recall that a subset of the nodes is called an independent set if no two of them are joined by an edge. Finding large independent sets is difficult in general; but here well see that it can be done efficiently if the graph is simple enough. Call a graph G =(V, E) a path if its nodes can be written as v1, v2, . . . , vn, with an edge between vi and vj if and only if the numbers i and j differ by exactly 1. With each node vi, we associate a positive integer weight wi. Consider, for example, the five-node path drawn in the image.

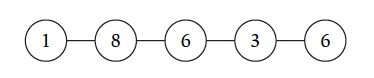
The weights are the numbers drawn inside the nodes. The goal in this question is to solve the following problem: Find an independent set in a path G whose total weight is as large as possible.

1) Problem Decomposition The recurrence for the maximum total weight OPT(n), together with a brief explanation how it is obtained.

2) The Algorithm The pseudocode of the bottom-up implementation of the dynamic programming algorithm based on the above recurrence, together with a brief analysis of its time complexity.

6 6