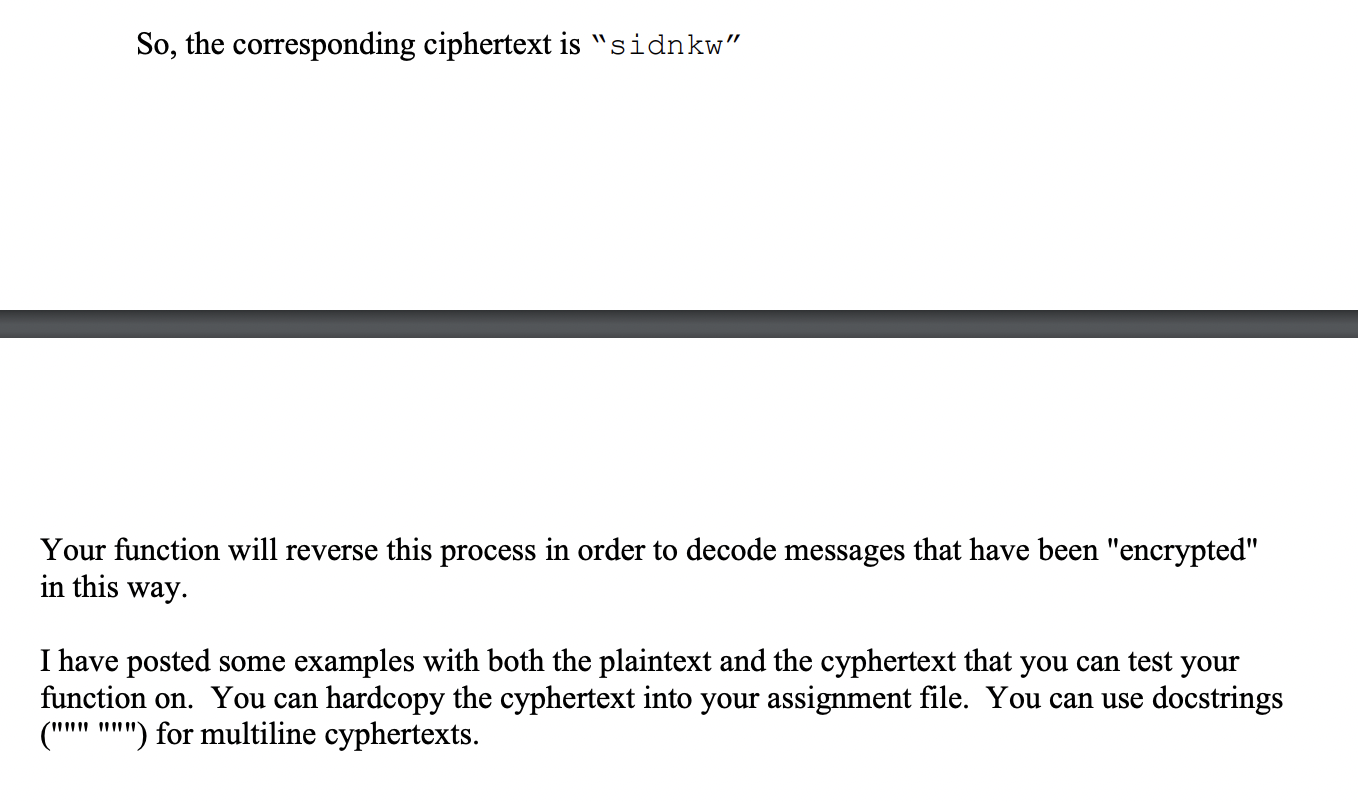
Function Description: Write a function, decode (), which takes a string of cyphertext (which is some encrypted English text) to a formal parameter named ct and returns a string of plaintext (which is the original English text that we can understand). The following encryption scheme is used: - The nth plaintext alphabetic letter, for n>1, is encrypted to the letter whose lexical position is the sum modulo 26 of the ordinal value of the nth letter with the sum of the ordinal values of all the letters that precede it in the plaintext. - The first plaintext alphabetic letter of the message is encrypted to the letter whose lexical position in the alphabet is the sum modulo 26 of the ordinal value of the first letter plus the integer 59. - Calculate the lexical position of the ciphertext letter as the letter at the position between 0 and 25, with ' a ' at 0, ' b ' at 1,, ' z ' at 25. - Calculate the ordinal value of a letter by passing the character to the ord () function. The integer returned is the ordinal value of the letter. - To simplify matters the only alphabetic characters contained in the plaintext message will be lowercase. No uppercase characters will be used. - Leave non-alphabetic characters, including whitespace, punctuation, numbers, etc. unchanged. Here is a small example: "secret" 1. The ordinal value of ' s ' is 115 . We compute 115+59=174(mod26)=18. The letter whose lexical position is 18 is ' s '. That's the first letter of the ciphertext. 2. The ordinal value of ' e ' is 101 . We compute 101+115 (the ordinal value of ' s ') =216 (mod26)=8. The letter whose lexical position is 8 is ' i '. That's the second letter of the ciphertext. 3. The ordinal value of ' c ' is 99 . We compute 99+(115+101) [the sum of the ordinal values of the preceding two plaintext letters ]=315(mod26)=3. The letter whose lexical position is 3 is ' d '. That's the third letter of the ciphertext. 4. ord(r)=114.114+115+101+99=429(mod26)=13 ' n ' 5. ord(e)=101.101+114+115+101+99=530(mod26)=10=> ' k ' 6. ord(t)=116.116+101+114+115+101+99=646(mod26)=22=> ' w ' So, the corresponding ciphertext is "sidnkw" Your function will reverse this process in order to decode messages that have been "encrypted" in this way. I have posted some examples with both the plaintext and the cyphertext that you can test your function on. You can hardcopy the cyphertext into your assignment file. You can use docstrings ("'"" ""') for multiline cyphertexts