Give a family of set cover problems where the set to be covered has n elements, the minimum set cover is size k = 3, and the greedy algorithm returns a cover of size (log n). That is, you should give a description of a set cover problem that works for a set of values of n that grows to infinity you might begin, for example, by saying, Consider the set 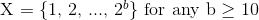, and consider subsets of X of the form..., and finish by saying We have shown that for the example above, the set cover returned by the greedy algorithm is of size b = (log n). (Your actual wording may differ substantially, of course, but this is the sort of thing were looking for.) Explain briefly how to generalize your construction for other (constant) values of k. (You need not give a complete proof of your generalization, but explain the types of changes needed from the case of k = 3.)