GIVE TYPED WRITING SO I CAN UNDERSTAND CLEARLY.

Hi,kindly reply with whole answers correct,accurate answers and step by step working.Do not skip step.Be very clear and mention about the formula for each step.Make sure the answers are correct and accurate. Be very organised with the working and systematic.Please explain to support and make it clear.

Answer all questions (including the ones with the wriiten working).Give answers and wrrking for the whole questions.

Number the answers according to the questions correctly based on each part.

PART 6:

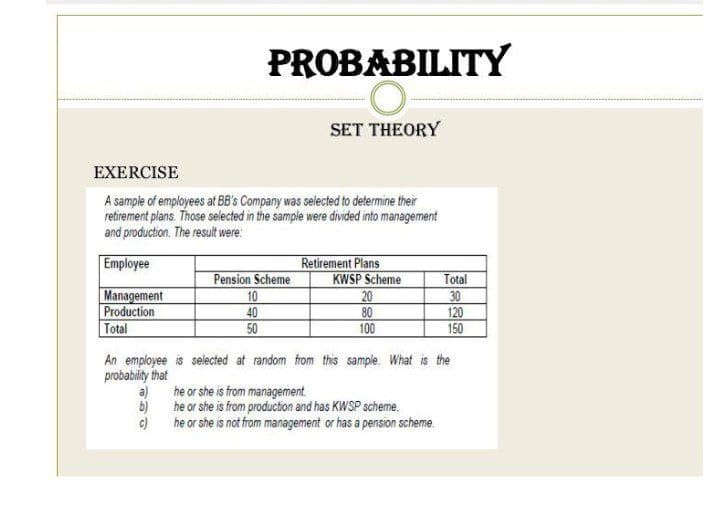
PROBABILITY O SET THEORY The Addition Rule: Non-Mutually Exclusive Example: In a certain town, 80% of the households own a car, 45% own a house and 35% own both a car and a home. Calculate the probability that a household in this town selected at random owns at least a car or a home. PROBABILITY O SET THEORY EXERCISE Given that P( X ) = 20 . P(Y ) = - and P(XUY)=, find a) P(XnY ) b) P(X|Y )PROBABILITY O SET THEORY EXERCISE A sample of employees at BB's Company was selected to determine their retirement plans. Those selected in the sample were divided into management and production. The result were Employee Retirement Plans Pension Scheme KWSP Scheme Total Management 10 20 30 Production 40 80 120 Total 50 100 150 An employee is selected at random from this sample. What is the probability that he or she is from management. he or she is from production and has KWSP scheme. he or she is not from management or has a pension scheme.PROBABILITY O SET THEORY EXERCISE Two events A and B are such that P (A) = 20 , P (B) = 25 25 - and P (A'0B) = Find P (An. B). P (An B). PROBABILITY O SET THEORY EXERCISE A student estimates that the probability that she will pass both her mathematics and finance final exams is 0.45. She also estimates that the probability that she will pass the finance final exam is 0.6. If the events of passing the two final exams are independent, (e What is the probability that she will pass the mathematics final exam? b) If the student discovers that she has passed the mathematics exam, what is the probability that she will pass the finance exam?PROBABILITY O INTRODUCTION TO PROBABILITY There are 8 Malaysians and 10 Indonesians candidates to be interviewed by ABC Sdn Bhd for 6 available positions. What is the probability of selecting 3 Indonesians candidate and 3 Malaysians candidate for that position? PROBABILITY O INTRODUCTION TO PROBABILITY There are 4 candidates from Tapah,5 candidates from Parit and 6 candidates from Ipoh in job interview at Bootstrap Resources. There have been summon for interview for 3 available positions at Decision Sciences Department. Find the probability that: a) 2 Candidates from Ipoh succeed for that position. b) One of each district candidates has succeeded the interview c) All three candidates from same district has succeed the interview.PROBABILITY O TREE DIAGRAM Example : A counselor classifies his students as excellent, fair and poor students based on the overall performance in their final examinations. Excellent and fair students constitute 10% and 30% of the students, respectively. The probability that a student will score A for mathematics for excellent, fair and poor students are 0.6, 0.3 and 0.1, respectively. a Draw a tree diagram to represent the above situation. Find the probability that a student chosen at random is classified as fair students and will score A for mathematics. C Find the probability that a student chosen at random will score A for mathematics. d) A student did not score A for his mathematics subject. What is the probability that he is an excellent student?BAYES THEOREM Example : In a certain assembly plant, three machine At,A2 and A3 make 30%.45% and 25% respectively of the products. It is known from past experience that 2%,3% and 2% of the product made by each machine respectively are defective. Now suppose that finished product is randomly selected. a) What is the probability it is defective? b) What is the probability that was made by machine A3