Given code, please finish in C++

#include

#include

#include

#include

#include

#include

#include

#include

#include

#include

#include

#include

#include

using namespace std;

/*

* A lexer node, representing one of the possible token types,

* as well as children in a recusrive manner when appropriate

*/

struct lexerNode {

enum type_t { BOOLEAN, INTEGER, NAME, EQUALS, SEQ } type;

string token;

vector children;

lexerNode(type_t type, const string &token, vector children = {}) :

type(type),

token(token),

children(move(children)) {}

};

/*

* A single program

*/

struct program {

vector> definitions;

vector expression;

};

/*

* Returns whether char 'c' is in the inclusive range: [l, r]

* This function just uses the numeric (ASCII) values for comparison

*/

bool inRange(char c, char l, char r) { return c >= l && c

/*

* Returns whether the specified 'test' string is present at 'index' in string 's'

*/

bool lookaheadEquals(const string s, int index, const string &test) { return s.substr(index, test.length()) == test; }

/*

* Returns the index of a matching pair of left/right characters (e.g. parens or braces),

* in `line`, starting with a left at `start`

*/

unsigned lookaheadMatch(const pair &leftRight, const string &line, unsigned start) {

unsigned s = 0;

for (unsigned i = start; i

if (line[i] == leftRight.first) {

++s;

} else if (line[i] == leftRight.second) {

if (--s == 0)

return i;

}

}

return start;

}

/*

* Possible fixed tokens

*/

vector> tokens{{lexerNode::EQUALS, "="}, {lexerNode::BOOLEAN, "TRUE"}, {lexerNode::BOOLEAN, "FALSE"}};

/*

* The possible left/right pairs we need to match (parens, braces, etc)

*/

vector> leftRights{{'(', ')'}, {'[', ']'}};

/*

* Returns an ordered sequence of lexer nodes for a given set of characters,

* representing some sort of expression

*/

vector lexExpression(const string &exprText) {

vector nodes;

optional<:type_t> type;

string token;

decltype(tokens)::iterator tokenIt;

for (unsigned i = 0; i

char c = exprText[i];

if (type) {

if ((c == ' ') || (c == '"')) {

nodes.emplace_back(*type, token);

type = nullopt;

token = "";

} else {

token += c;

}

} else {

if (c == ' ') {

continue;

} else if ((tokenIt = find_if(tokens.begin(), tokens.end(), [&](auto token) { return lookaheadEquals(exprText, i, token.second); })) != tokens.end()) {

nodes.emplace_back(tokenIt->first, tokenIt->second);

i += tokenIt->second.size() - 1;

} else if (inRange(c, '0', '9') || c == '-') {

type = lexerNode::INTEGER;

token += c;

} else if (inRange(c, 'a', 'z') || inRange(c, 'A', 'Z')) {

type = lexerNode::NAME;

token += c;

} else {

auto leftRightIt = find_if(leftRights.begin(), leftRights.end(), [c](const auto &leftRight) { return c == leftRight.first; });

if (leftRightIt != leftRights.end()) {

unsigned matchingRightIndex = lookaheadMatch(*leftRightIt, exprText, i);

nodes.emplace_back(lexerNode::SEQ, string(1, leftRightIt->first), lexExpression(exprText.substr(i + 1, matchingRightIndex - i - 1)));

i = matchingRightIndex + 1;

}

}

}

}

if (type)

nodes.emplace_back(*type, token);

return nodes;

}

/*

* Returns a program parsed from a stream

*/

program lexProgram(istream &in) {

vector> defines;

vector expr;

string line;

while (getline(in, line)) {

if (line.empty())

continue;

if (!expr.empty())

defines.emplace_back(move(expr));

expr = lexExpression(line);

}

return program{defines, expr};

}

int main() {

program p = lexProgram(cin);

return 0;

}

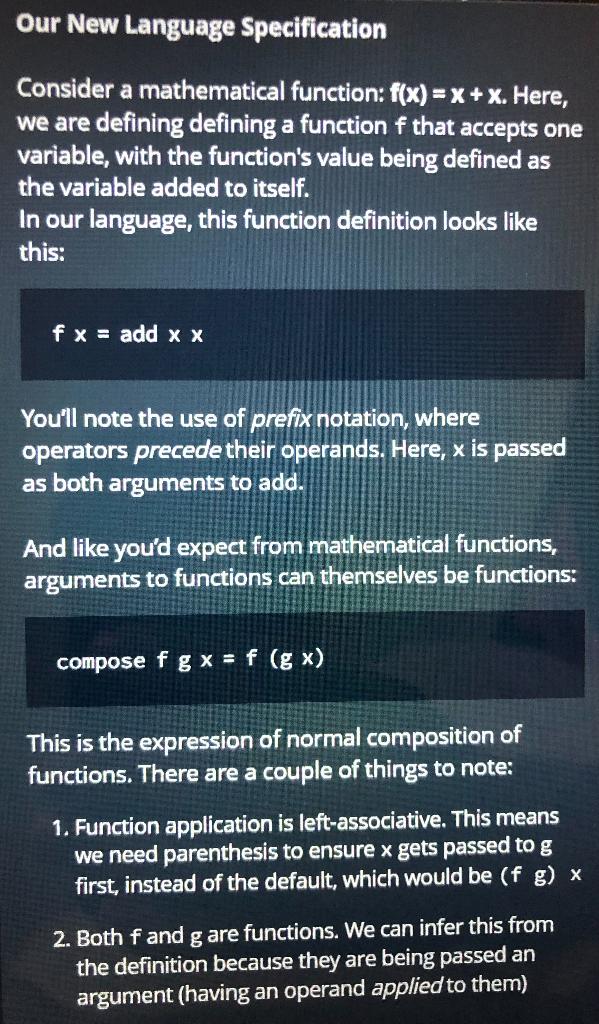
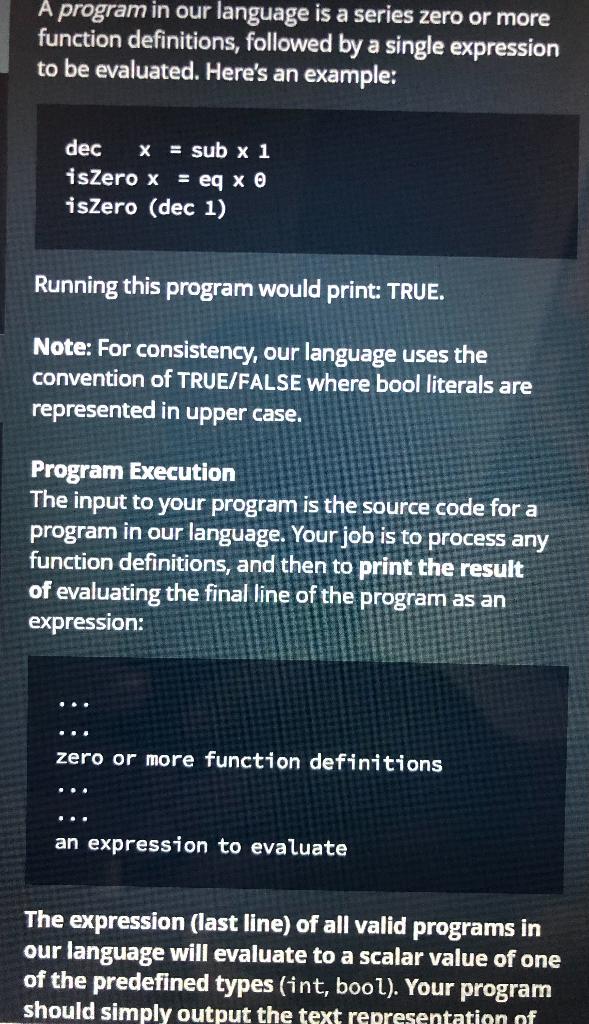
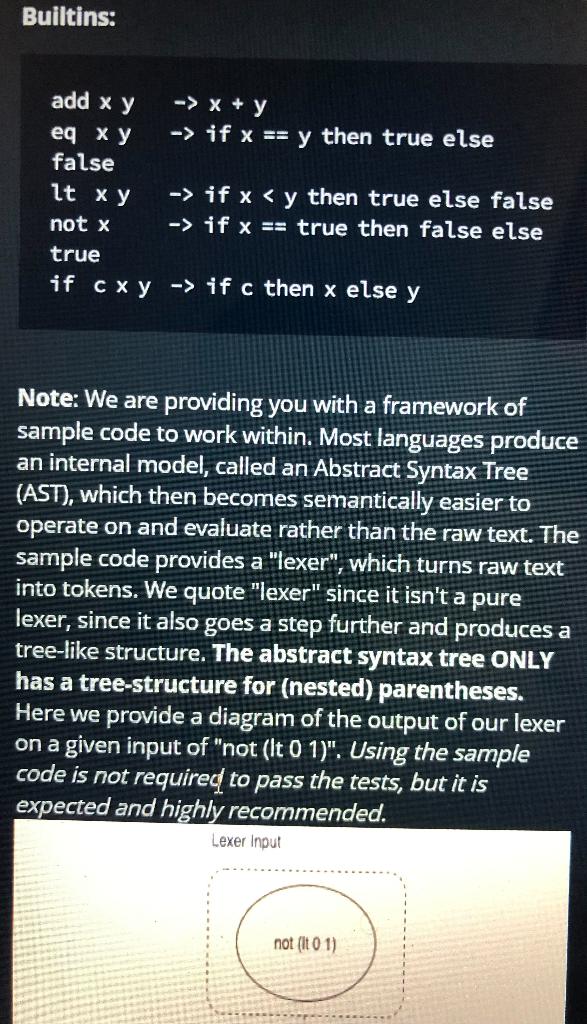
Our New Language Specification Consider a mathematical function: f(x) = x + X. Here, we are defining defining a function f that accepts one variable, with the function's value being defined as the variable added to itself. In our language, this function definition looks like this: fx = add x x You'll note the use of prefix notation, where operators precede their operands. Here, x is passed as both arguments to add. And like you'd expect from mathematical functions, arguments to functions can themselves be functions: compose f g x = f (g x) This is the expression of normal composition of functions. There are a couple of things to note: 1. Function application is left-associative. This means we need parenthesis to ensure x gets passed to g first, instead of the default, which would be (f g) x 2. Both fand g are functions. We can infer this from the definition because they are being passed an argument (having an operand applied to them) A program in our language is a series zero or more function definitions, followed by a single expression to be evaluated. Here's an example: dec x = sub x1 isZero x = eq x isZero (dec 1) Running this program would print: TRUE. Note: For consistency, our language uses the convention of TRUE/FALSE where bool literals are represented in upper case. Program Execution The input to your program is the source code for a program in our language. Your job is to process any function definitions, and then to print the result of evaluating the final line of the program as an expression: ... zero or more function definitions ... an expression to evaluate The expression (last line) of all valid programs in our language will evaluate to a scalar value of one of the predefined types (int, bool). Your program should simply output the text representation of should simply output the text representation of that scalar. You are also guaranteed that all programs will be valid and pass valid arguments. You do not need to do any error checking or validation. Note: We recommend that you write and test your code using the HackerRank web interface. On the other hand, if you prefer to run your interpreter program on the command line you'll have to type CTRL-D after all of the functional code is entered into stdin to signal that the input is completed. The HackerRank tester does this automatically. There is no code for Part 0. Part 1: Built-ins and Basic Application Because our language is simple, we must provide some "standard" or "built-in" functions upon which to base our own programs. Your built-in functions represent the basis upon which other programs can be built. The set we would like you to implement for this part is listed below. implement an interpreter that executes one pragaras composed of any of the builtin ettons listed below. Builtins: Builtins: add x y lt X -> x + y -> if x == y then true else false -> if x if x == true then false else true if cxy-> if c then x else y Note: We are providing you with a framework of sample code to work within. Most languages produce an internal model, called an Abstract Syntax Tree (AST), which then becomes semantically easier to operate on and evaluate rather than the raw text. The sample code provides a "lexer", which turns raw text into tokens. We quote "lexer" since it isn't a pure lexer, since it also goes a step further and produces a tree-like structure. The abstract syntax tree ONLY has a tree-structure for (nested) parentheses. Here we provide a diagram of the output of our lexer on a given input of "not (lt 0 1)". Using the sample code is not required to pass the tests, but it is expected and highly recommended. Lexer Input not (It 01) Our New Language Specification Consider a mathematical function: f(x) = x + X. Here, we are defining defining a function f that accepts one variable, with the function's value being defined as the variable added to itself. In our language, this function definition looks like this: fx = add x x You'll note the use of prefix notation, where operators precede their operands. Here, x is passed as both arguments to add. And like you'd expect from mathematical functions, arguments to functions can themselves be functions: compose f g x = f (g x) This is the expression of normal composition of functions. There are a couple of things to note: 1. Function application is left-associative. This means we need parenthesis to ensure x gets passed to g first, instead of the default, which would be (f g) x 2. Both fand g are functions. We can infer this from the definition because they are being passed an argument (having an operand applied to them) A program in our language is a series zero or more function definitions, followed by a single expression to be evaluated. Here's an example: dec x = sub x1 isZero x = eq x isZero (dec 1) Running this program would print: TRUE. Note: For consistency, our language uses the convention of TRUE/FALSE where bool literals are represented in upper case. Program Execution The input to your program is the source code for a program in our language. Your job is to process any function definitions, and then to print the result of evaluating the final line of the program as an expression: ... zero or more function definitions ... an expression to evaluate The expression (last line) of all valid programs in our language will evaluate to a scalar value of one of the predefined types (int, bool). Your program should simply output the text representation of should simply output the text representation of that scalar. You are also guaranteed that all programs will be valid and pass valid arguments. You do not need to do any error checking or validation. Note: We recommend that you write and test your code using the HackerRank web interface. On the other hand, if you prefer to run your interpreter program on the command line you'll have to type CTRL-D after all of the functional code is entered into stdin to signal that the input is completed. The HackerRank tester does this automatically. There is no code for Part 0. Part 1: Built-ins and Basic Application Because our language is simple, we must provide some "standard" or "built-in" functions upon which to base our own programs. Your built-in functions represent the basis upon which other programs can be built. The set we would like you to implement for this part is listed below. implement an interpreter that executes one pragaras composed of any of the builtin ettons listed below. Builtins: Builtins: add x y lt X -> x + y -> if x == y then true else false -> if x if x == true then false else true if cxy-> if c then x else y Note: We are providing you with a framework of sample code to work within. Most languages produce an internal model, called an Abstract Syntax Tree (AST), which then becomes semantically easier to operate on and evaluate rather than the raw text. The sample code provides a "lexer", which turns raw text into tokens. We quote "lexer" since it isn't a pure lexer, since it also goes a step further and produces a tree-like structure. The abstract syntax tree ONLY has a tree-structure for (nested) parentheses. Here we provide a diagram of the output of our lexer on a given input of "not (lt 0 1)". Using the sample code is not required to pass the tests, but it is expected and highly recommended. Lexer Input not (It 01)