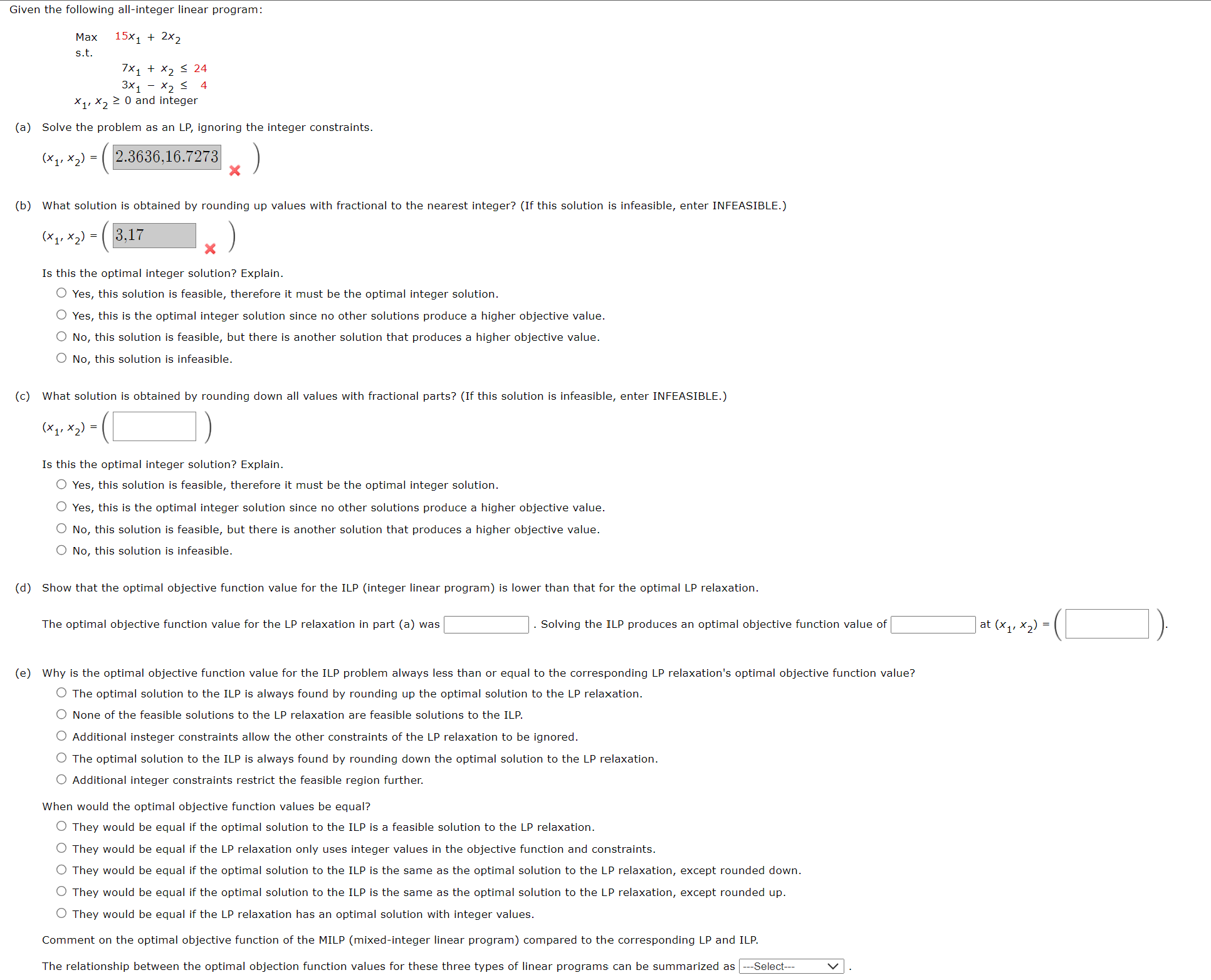Given the following all-integer linear program: Maxs.t.x1,x20andinteger15x1+2x27x1+x2243x1x24 (a) Solve the problem as an LP, ignoring the integer constraints. (x1,x2)=(x) (b) What solution is obtained by rounding up values with fractional to the nearest integer? (If this solution is infeasible, enter INFEASIBLE.) (x1,x2)=(x) Is this the optimal integer solution? Explain. Yes, this solution is feasible, therefore it must be the optimal integer solution. Yes, this is the optimal integer solution since no other solutions produce a higher objective value. No, this solution is feasible, but there is another solution that produces a higher objective value. No, this solution is infeasible. (c) What solution is obtained by rounding down all values with fractional parts? (If this solution is infeasible, enter INFEASIBLE.) (x1,x2)=() Is this the optimal integer solution? Explain. Yes, this solution is feasible, therefore it must be the optimal integer solution. Yes, this is the optimal integer solution since no other solutions produce a higher objective value. No, this solution is feasible, but there is another solution that produces a higher objective value. No, this solution is infeasible. (d) Show that the optimal objective function value for the ILP (integer linear program) is lower than that for the optimal LP relaxation. The optimal objective function value for the LP relaxation in part (a) was . Solving the ILP produces an optimal objective function value of at(x1,x2)=(). (e) Why is the optimal objective function value for the ILP problem always less than or equal to the corresponding LP relaxation's optimal objective function value? The optimal solution to the ILP is always found by rounding up the optimal solution to the LP relaxation. None of the feasible solutions to the LP relaxation are feasible solutions to the ILP. Additional insteger constraints allow the other constraints of the LP relaxation to be ignored. The optimal solution to the ILP is always found by rounding down the optimal solution to the LP relaxation. Additional integer constraints restrict the feasible region further. When would the optimal objective function values be equal? They would be equal if the optimal solution to the ILP is a feasible solution to the LP relaxation. They would be equal if the LP relaxation only uses integer values in the objective function and constraints. They would be equal if the optimal solution to the ILP is the same as the optimal solution to the LP relaxation, except rounded down. They would be equal if the optimal solution to the ILP is the same as the optimal solution to the LP relaxation, except rounded up. They would be equal if the LP relaxation has an optimal solution with integer values. Comment on the optimal objective function of the MILP (mixed-integer linear program) compared to the corresponding LP and ILP