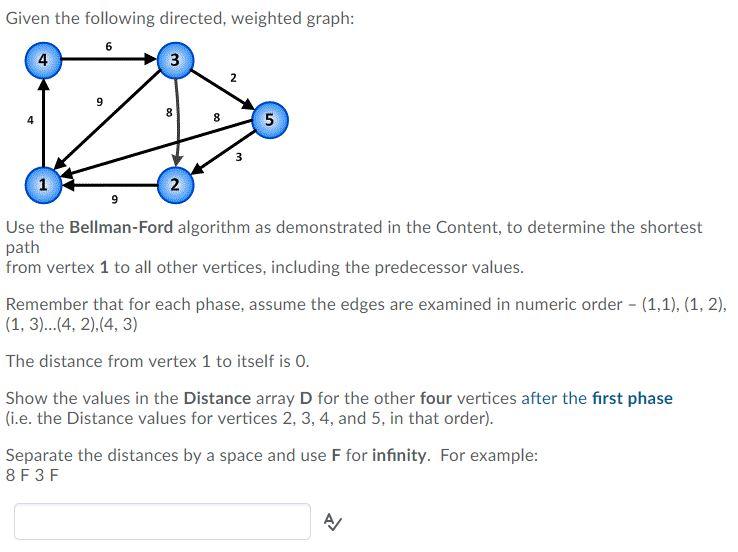
Given the following directed, weighted graph: 6 4 3 2 8 8 5 3 2 9 Use the Bellman-Ford algorithm as demonstrated in the Content, to determine the shortest path from vertex 1 to all other vertices, including the predecessor values. Remember that for each phase, assume the edges are examined in numeric order - (1,1), (1, 2), (1, 3)...(4, 2),(4,3) The distance from vertex 1 to itself is O. Show the values in the Distance array D for the other four vertices after the first phase (i.e. the Distance values for vertices 2, 3, 4, and 5, in that order). Separate the distances by a space and use F for infinity. For example: 8 F3 F A/