Question
Given the regular expression ((a|b) (a|bb))* (a) Construct an equivalent NFA using the method in Sect. (b) Convert this NFA to a DFA using Algorithm
Given the regular expression ((a|b) (a|bb))* (a) Construct an equivalent NFA using the method in Sect. (b) Convert this NFA to a DFA using Algorithm
shows an example of a nondeterministic finite automaton having three States. State 1 is the starting state, and state 3 is accepting. There is an epsilontransition from state 1 to state 2, transitions on the symbol a fromstate 2 to states 1 and 3, and a transition on the symbol b from state 1 to state 3. This NFA recognises the language described by the regular expression a (a|b). As an example, the string aab is recognised by the following sequence of transitions:
from to by
1 2 2 1 a 1 2 2 1 a 1 3 b At the end of the input we are in state 3, which is accepting. Hence, the string is accepted by the NFA. You can check this by placing a coin at the starting state and follow the transitions by moving the coin. Note that we sometimes have a choice of several transitions. If we are in state 2 and the next symbol is an a, we can, when reading this, either go to state 1 or to state 3. Likewise, if we are in state 1 and the next symbol is a b, we can either read this and go to state 3, or we can use the epsilon transition to go directly to state 2 without reading anything. If we, in the example above, had chosen to follow the a-transition to state 3 instead of state 1, we would have been stuck: We would have no legal transition, and yet we would not be at the end of the input. But, as previously stated, it is enough that there exists a path leading to acceptance, so the string aab is accepted by the NFA. A program that decides if a string is accepted by a given NFA will have to check all possible paths to see if any of these accepts the string. This requires either backtracking until a successful path found, or simultaneously following all possible paths. Both of these methods are too time-consuming to make NFAs suitable for efficient recognisers. We will, hence, use NFAs only as a stepping stone between regular expressions and the more efficient DFAs. We use this stepping stone because it makes the construction simpler than direct construction of a DFA from a regular expression.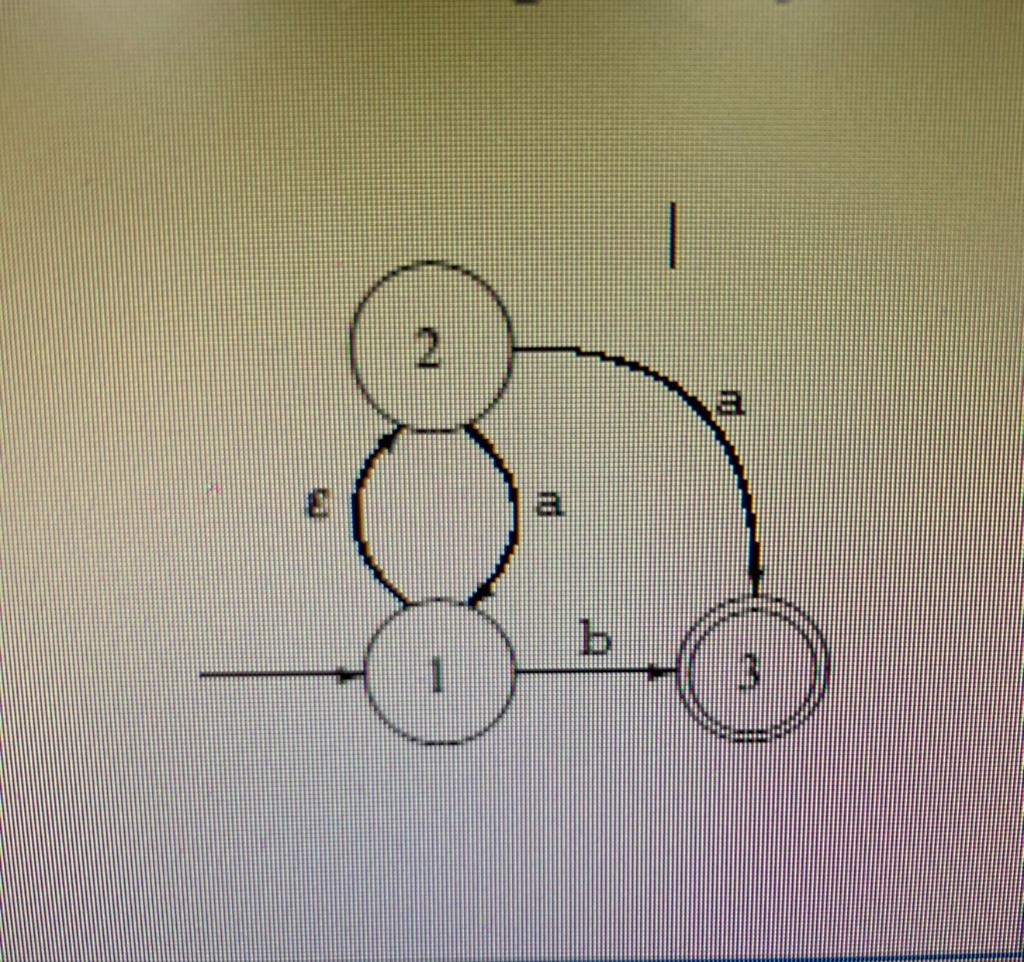
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


