Given the R(j omega) you derived, what needs to be done to restore the original signal?

This is what I've derived for r(t):

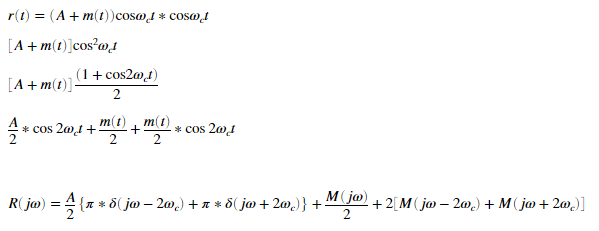
Below is the MATLAB comments on the "amdemod" function:

function z = amdemod(y, Fc, Fs, ini_phase, varargin) %AMDEMOD Amplitude demodulation. % Z = AMDEMOD(Y,Fc,Fs) demodulates the amplitude modulated signal Y from % the carrier frequency Fc (Hz). Y and Fc have sample frequency Fs (Hz). % The modulated signal Y has zero initial phase, and zero carrier % amplitude, for suppressed carrier modulation. A lowpass filter is used % in the demodulation. The default filter is: [NUM,DEN] = % butter(5,Fc*2/Fs). % % Z = AMDEMOD(Y,Fc,Fs,INI_PHASE) specifies the initial phase (rad) of the % modulated signal. % % Z = AMDEMOD(Y,Fc,Fs,INI_PHASE,CARRAMP) specifies the carrier amplitude % of the modulated signal for transmitted carrier modulation. % % Z = AMDEMOD(Y,Fc,Fs,INI_PHASE,CARRAMP,NUM,DEN) specifies the filter to % be used in the demodulation. % % See also AMMOD, SSBDEMOD, FMDEMOD, PMDEMOD.

% Copyright 1996-2011 The MathWorks, Inc.

% Number of arguments check if(nargin > 7) error(message('comm:amdemod:tooManyInp')); end

%Check y,Fc, Fs, ini_phase, numerator and denominator. if(~isreal(y)|| ~isnumeric(y)) error(message('comm:amdemod:Yreal')); end

if(~isreal(Fc) || ~isscalar(Fc) || Fc

if(~isreal(Fs) || ~isscalar(Fs) || Fs

% check that Fs must be greater than 2*Fc if(Fs

if(nargin

carr_amp = 0; % check the carrier amplitude if(nargin>=5) carr_amp = varargin{1}; if(isempty(carr_amp)) carr_amp = 0; elseif(~isreal(carr_amp) || ~isscalar(carr_amp)|| ~isnumeric(carr_amp)) error(message('comm:amdemod:carrAmpReal')) end end

if(isempty(varargin)|| nargin == 5) [num,den] = butter(5,Fc*2/Fs); % check that the numerator and denominator are valid, and come in a pair elseif( (nargin == 6) ) error(message('comm:amdemod:numDenPair')); % check to make sure that both num and den have values. elseif( xor( isempty(varargin{2}), isempty(varargin{3}))) error(message('comm:amdemod:numDenPair')); elseif( isempty(varargin{2}) && isempty(varargin{3}) ) [num,den] = butter(5,Fc*2/Fs); else num = varargin{2}; den = varargin{3}; end

% --- Assure that Y, if one dimensional, has the correct orientation --- % wid = size(y,1); if(wid ==1) y = y(:); end

t = (0 : 1/Fs :(size(y,1)-1)/Fs)'; t = t(:, ones(1, size(y, 2))); z = y .* cos(2*pi * Fc * t + ini_phase); for i = 1 : size(y, 2) z(:, i) = filtfilt(num, den, z(:, i)) * 2; end

z = z - carr_amp;

% --- restore the output signal to the original orientation --- % if(wid == 1) z = z'; end

% --- EOF --- % >>

5. Given the R(jw) you derived, what needs to be done to restore the original signal? In the MATLAB command window, type "type amdemod". It will display the script for the demodulation function. Read the code and describe the demodulation process. How is the signal restored to its original form? Does the procedure make sense based on the R(jw) you derived? The script uses a butterworth low pass filter. What is the default cutoff frequency? Why is it a good choice? Refer to the MATLAB documentation (you can type "help butter" at the command line) or noise removal lab for the syntax of "butter" command. r(t) = (A +mt) cosm.1 * cose1 [A +m(1) cosa 1 [A +m(0) 1 + cs208) 4 + cos 2004+ mO + ml + cos 2014 R(jo) = 4{** 8( jo 20.) +A* 8ju +20)} + M ) + 2[M( jo 20.) +Mj +20)] 5. Given the R(jw) you derived, what needs to be done to restore the original signal? In the MATLAB command window, type "type amdemod". It will display the script for the demodulation function. Read the code and describe the demodulation process. How is the signal restored to its original form? Does the procedure make sense based on the R(jw) you derived? The script uses a butterworth low pass filter. What is the default cutoff frequency? Why is it a good choice? Refer to the MATLAB documentation (you can type "help butter" at the command line) or noise removal lab for the syntax of "butter" command. r(t) = (A +mt) cosm.1 * cose1 [A +m(1) cosa 1 [A +m(0) 1 + cs208) 4 + cos 2004+ mO + ml + cos 2014 R(jo) = 4{** 8( jo 20.) +A* 8ju +20)} + M ) + 2[M( jo 20.) +Mj +20)]