Given this greedy Max-Cut algorithm:

Answer the following two questions:

a)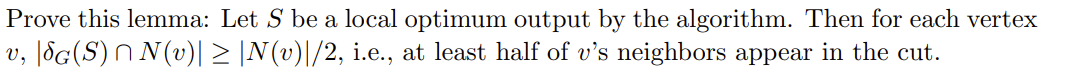

b)

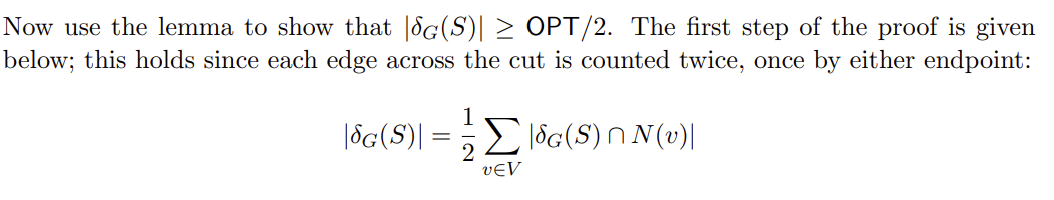Let G=(V,E) be an undirected, unweighted graph. In MAXCUT, the goal is to partition V into (S,V\S) so as to maximize the number of edges crossing S, that is G(S). Consider the following greedy local-search algorithm to find a MAXCUT: Initially S=. We apply the following steps in each iteration until the algorithm terminates. (a) If there is a vertex vV\S s.t. G(S{v})>G(S), update S:=S{v}. (b) Else, if is a vertex vS s.t. G(S\{v})>G(S), update S:=S\{v}. (c) If neither of the previous conditions applied, then S is a local optimum, so return S. Prove this lemma: Let S be a local optimum output by the algorithm. Then for each vertex v,G(S)N(v)N(v)/2, i.e., at least half of v 's neighbors appear in the cut. Now use the lemma to show that G(S)OPT/2. The first step of the proof is given below; this holds since each edge across the cut is counted twice, once by either endpoint: G(S)=21vVG(S)N(v)