Golden Section Search in Python 3

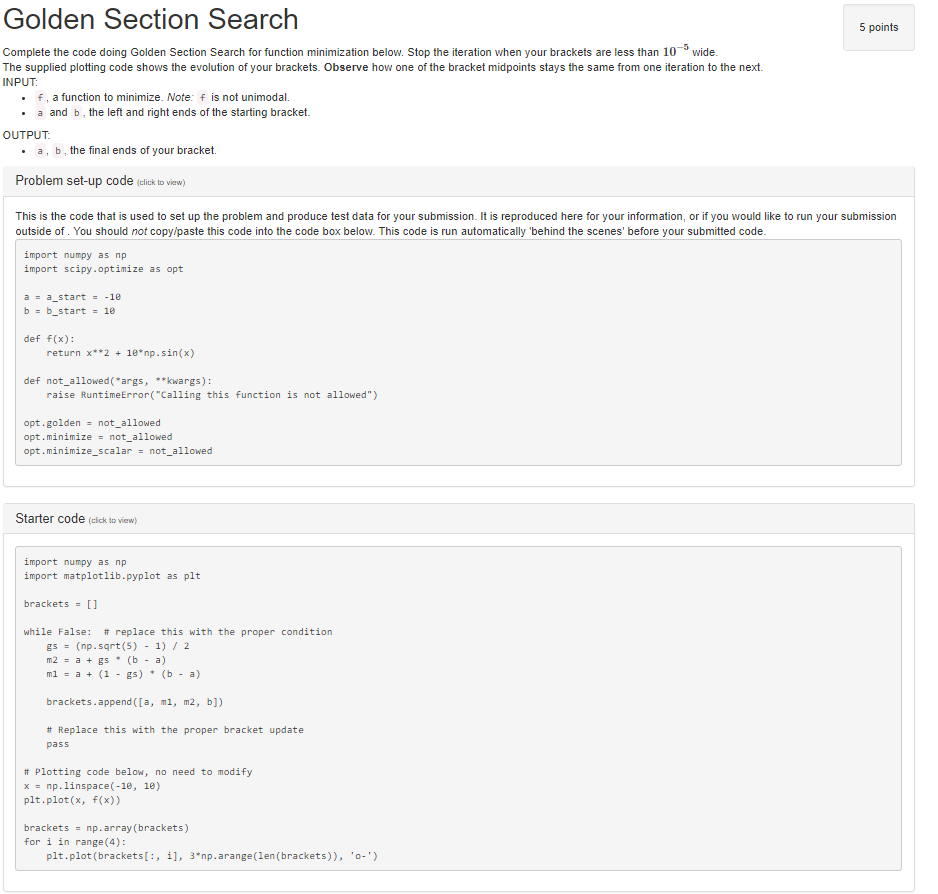
Golden Section Search 5 points Complete the code doing Golden Section Search for function minimization below. Stop the iteration when your brackets are less than 10 wide The supplied plotting code shows the evolution of your brackets. Observe how one of the bracket midpoints stays the same from one iteration to the next INPUT f, a function to minimize. Note: f is not unimodal. . .a and b, the left and right ends of the starting bracket. . a, b, the final ends of your bracket. Problem set-up code (click to view) OUTPUT This is the code that is used to set up the problem and produce test data for your submission. It is reproduced here for your information, or if you would like to run your submission outside of. You should not copy/paste this code into the code box below. This code is run automatically 'behind the scenes' before your submitted code. import numpy as np import scipy.optimize as opt a-a start -18 def f(x): return x2 18 np.sin(x) def not_allowed( args, **kwargs): raise RuntimeError( "Calling this function is not allowed") opt.golden not_allowed opt.minimize not_allowed opt . minimize-scalar not-allowed Starter code (cick to view) import numpy as np import matplotlib.pyplot as plt brackets[] while False: # replace this with the proper condition gs-(np.sqrt (5)- 1) 2 ml a (1 gs)(b a) brackets.append (a, mi, m2, b]) # Replace this with the proper bracket update pass Plotting code below, no need to modify x np.linspace(-10, 10) plt.plot (x, f(x)) bracketsnp.array (brackets) for i in range(4): plt.plot (brackets[:, i, 3"np.arange(len (brackets)), 0- Golden Section Search 5 points Complete the code doing Golden Section Search for function minimization below. Stop the iteration when your brackets are less than 10 wide The supplied plotting code shows the evolution of your brackets. Observe how one of the bracket midpoints stays the same from one iteration to the next INPUT f, a function to minimize. Note: f is not unimodal. . .a and b, the left and right ends of the starting bracket. . a, b, the final ends of your bracket. Problem set-up code (click to view) OUTPUT This is the code that is used to set up the problem and produce test data for your submission. It is reproduced here for your information, or if you would like to run your submission outside of. You should not copy/paste this code into the code box below. This code is run automatically 'behind the scenes' before your submitted code. import numpy as np import scipy.optimize as opt a-a start -18 def f(x): return x2 18 np.sin(x) def not_allowed( args, **kwargs): raise RuntimeError( "Calling this function is not allowed") opt.golden not_allowed opt.minimize not_allowed opt . minimize-scalar not-allowed Starter code (cick to view) import numpy as np import matplotlib.pyplot as plt brackets[] while False: # replace this with the proper condition gs-(np.sqrt (5)- 1) 2 ml a (1 gs)(b a) brackets.append (a, mi, m2, b]) # Replace this with the proper bracket update pass Plotting code below, no need to modify x np.linspace(-10, 10) plt.plot (x, f(x)) bracketsnp.array (brackets) for i in range(4): plt.plot (brackets[:, i, 3"np.arange(len (brackets)), 0