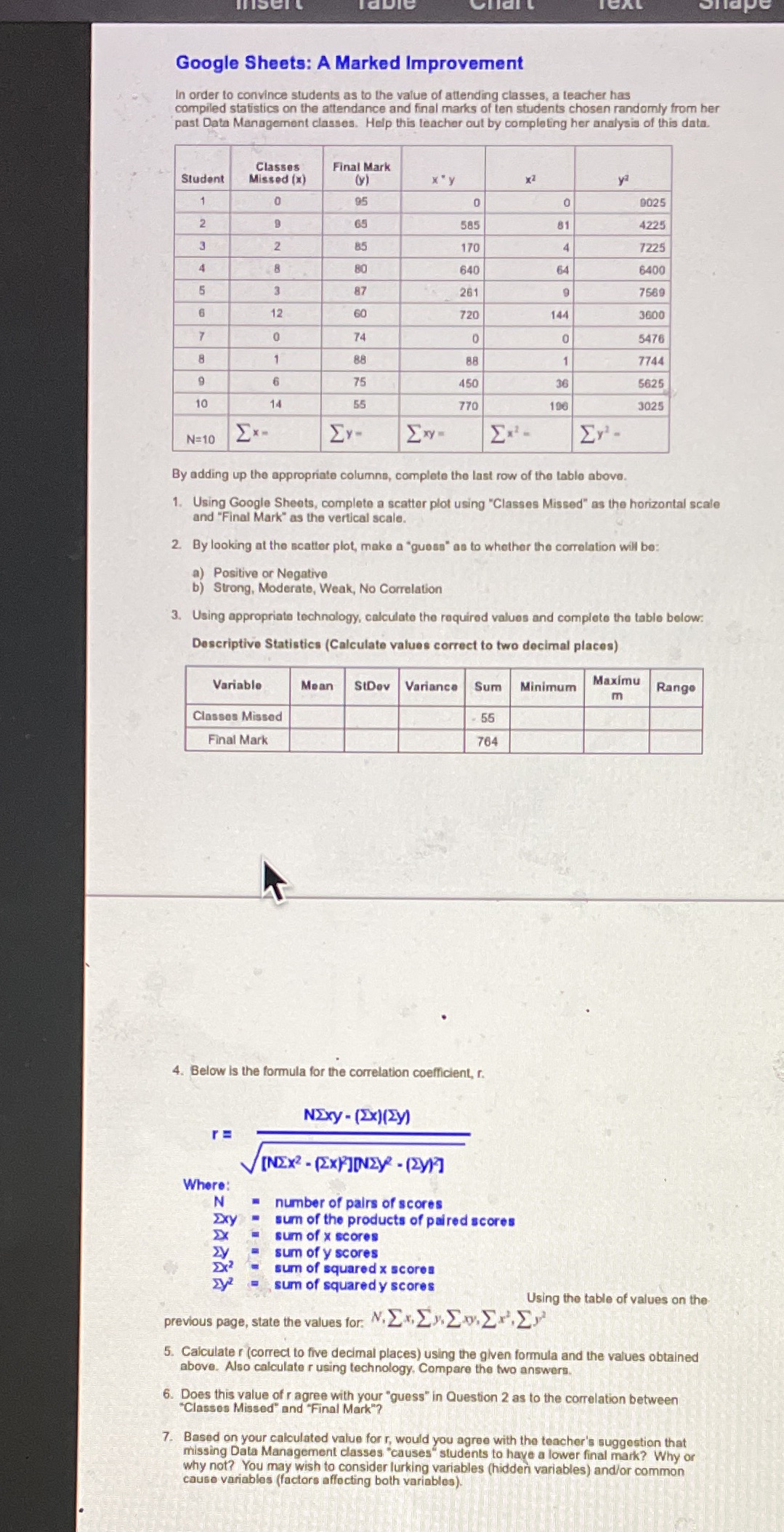
Google Sheets: A Marked Improvement In order to convince students as to the value of attending classes, a teacher has compiled statistics on the attendance and final marks of ten students chosen randomly from her past Data Management classes. Help this teacher out by completing her analysis of this data. Classes Final Mark Student Missed (x) X 'y XZ 0 95 0 0 DO25 2 65 585 81 $225 3 2 85 170 4 7225 4 8 80 640 64 640 3 87 261 9 7589 6 12 60 720 144 360 7 0 74 0 0 5476 8 1 88 88 1 7744 9 6 75 450 36 5625 10 14 55 770 196 3025 N=10 Ex- Ex- By adding up the appropriate columns, complete the last row of the table above. 1. Using Google Sheets, complete a scatter plot using "Classes Missed" as the horizontal scale and "Final Mark" as the vertical scale. 2. By looking at the scatter plot, make a "guess" as to whether the correlation will be: a) Positive or Negative b) Strong, Moderate, Weak, No Correlation 3. Using appropriate technology, calculate the required values and complete the table below. Descriptive Statistics (Calculate values correct to two decimal places) Variable Mean StDev Variance Sum Minimum Maximu Range m Classes Missed 56 Final Mark 764 4. Below is the formula for the correlation coefficient, r. NExy - (Xx)(>y) r= [NEX2 - (EXPJINZy - (>y)] Where: N number of pairs of scores xxy sum of the products of paired scores EX sum of x scores zy sum of y scores sum of squared x scores sum of squared y scores Using the table of values on the previous page, state the values for: N. Ex. Ev.Ex..EP. 5. Calculate r (correct to five decimal places) using the given formula and the values obtained above. Also calculate r using technology. Compare the two answers. 6. Does this value of r agree with your "guess" in Question 2 as to the correlation between "Classes Missed" and "Final Mark"? 7. Based on your calculated value for r, would you agree with the teacher's suggestion that missing Data Management classes "causes" students to have a lower final mark? Why or why not? You may wish to consider lurking variables (hidden variables) and/or common cause variables (factors affecting both variables)