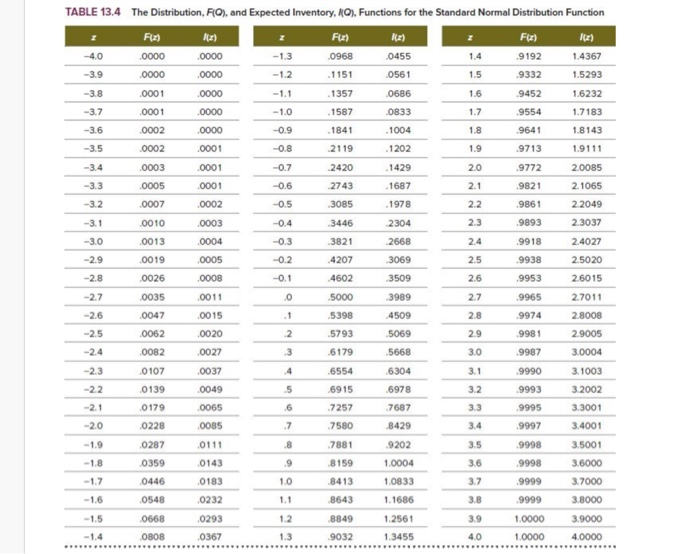
Goop Inc. needs to order a raw material to make a special polymer. The demand for the polymer is forecasted to be normally distributed with a mean of 320 gallons and a standard deviation of 135 gallons. Goop sells the polymer for $24 per gallon. Goop purchases raw material for $12 per gallon and must spend $3 per gallon to dispose of all unused raw material due to government regulations. (One gallon of raw material yields one gallon of polymer.) If demand is more than Goop can make, then Goop sells only what it has made, and the rest of the demand is lost. Round your answer to 2 digits after the decimal point if it is not an integer. Do NOT use comma in your numeric answers. The average cost is $ The underage cost is $ The critical ratio is Goop Inc. should order gallons of this raw material to maximize its expected profit. In such case, the expected leftover inventory will be gallons, the expected sales will be gallons, and the expected profit will be $ (use the standard normal table below) The maximum profit of Goop Inc. is $ If Goop Inc. orders 360 gallons, then the in-stock probability will be %, the expected leftover inventory will be gallons, the expected profit will be $ and the mismatch cost will be $ (use the standard normal table below). -4.0 22 TABLE 13.4 The Distribution, FQ), and Expected Inventory, 19), Functions for the Standard Normal Distribution Function F(2) Fiz) F42) (2) .0000 .0000 -1.3 0968 .0455 1.4 9192 1.4367 -3.9 .0000 .0000 -1.2 . 1151 .0561 1.5 .9332 1.5293 -3.8 .0001 .0000 -1.1 . 1357 .0686 1.6 9452 1.6232 -3.7 .0001 .0000 -1.0 1587 0833 1.7 9554 1.7183 -3.6 .0002 .0000 -0.9 .1841 .1004 1.8 9641 1.8143 -3.5 .0002 .0001 -0.8 2119 .1202 1.9 9713 1.9111 -3.4 0003 .0001 -0.7 2420 .1429 2.0 9772 2.0085 -3.3 .0005 0001 -0.6 2743 . 1687 2.1 .9821 2. 1065 -3.2 .0007 .0002 -0.5 3085 .1978 .9861 22049 -3.1 0010 0003 -0.4 3446 2304 2.3 9893 2.3037 -3.0 .0013 .0004 -0.3 3821 2668 2.4 9918 2.4027 -2.9 .0019 .0005 -0.2 .4207 3069 2.5 .9938 2.5020 -2.8 0026 .0008 -0.1 4602 3509 26 .9953 2.6015 -2.7 .0035 .0011 .0 .5000 3989 2.7 9965 2.7011 -2.6 .0047 .0015 .1 5398 .4509 2.8 .9974 2.8008 -2.5 0062 0020 2 .5793 5069 2.9 9981 2.9005 -2.4 0082 .0027 3 .6179 .5668 3.0 9987 3.0004 -2.3 0107 0037 4 .6554 .6304 3.1 .9990 3.1003 -22 0139 0049 5 .6915 .6978 3.2 9993 3.2002 -2.1 0179 .0065 6 .7257 .7687 33 9995 3.3001 -2.0 0228 0085 .7 .7580 8429 3.4 .9997 3.4001 -1.9 0287 8 .9202 3.5 9998 3.5001 0111 0143 -1.8 .9 .7881 8159 8413 0359 0446 .9998 3.6 3.7 -1.7 1.0 0183 0232 1.0004 1.0833 1.1686 1.2561 .9999 9999 0548 1.1 3.8 3.6000 3.7000 3.8000 3.9000 4.0000 -1.5 0293 1.2 8643 8849 9032 0668 0808 3.9 1.0000 1.0000 -1.4 .0367 1.3 1.3455 4.0 Goop Inc. needs to order a raw material to make a special polymer. The demand for the polymer is forecasted to be normally distributed with a mean of 320 gallons and a standard deviation of 135 gallons. Goop sells the polymer for $24 per gallon. Goop purchases raw material for $12 per gallon and must spend $3 per gallon to dispose of all unused raw material due to government regulations. (One gallon of raw material yields one gallon of polymer.) If demand is more than Goop can make, then Goop sells only what it has made, and the rest of the demand is lost. Round your answer to 2 digits after the decimal point if it is not an integer. Do NOT use comma in your numeric answers. The average cost is $ The underage cost is $ The critical ratio is Goop Inc. should order gallons of this raw material to maximize its expected profit. In such case, the expected leftover inventory will be gallons, the expected sales will be gallons, and the expected profit will be $ (use the standard normal table below) The maximum profit of Goop Inc. is $ If Goop Inc. orders 360 gallons, then the in-stock probability will be %, the expected leftover inventory will be gallons, the expected profit will be $ and the mismatch cost will be $ (use the standard normal table below). -4.0 22 TABLE 13.4 The Distribution, FQ), and Expected Inventory, 19), Functions for the Standard Normal Distribution Function F(2) Fiz) F42) (2) .0000 .0000 -1.3 0968 .0455 1.4 9192 1.4367 -3.9 .0000 .0000 -1.2 . 1151 .0561 1.5 .9332 1.5293 -3.8 .0001 .0000 -1.1 . 1357 .0686 1.6 9452 1.6232 -3.7 .0001 .0000 -1.0 1587 0833 1.7 9554 1.7183 -3.6 .0002 .0000 -0.9 .1841 .1004 1.8 9641 1.8143 -3.5 .0002 .0001 -0.8 2119 .1202 1.9 9713 1.9111 -3.4 0003 .0001 -0.7 2420 .1429 2.0 9772 2.0085 -3.3 .0005 0001 -0.6 2743 . 1687 2.1 .9821 2. 1065 -3.2 .0007 .0002 -0.5 3085 .1978 .9861 22049 -3.1 0010 0003 -0.4 3446 2304 2.3 9893 2.3037 -3.0 .0013 .0004 -0.3 3821 2668 2.4 9918 2.4027 -2.9 .0019 .0005 -0.2 .4207 3069 2.5 .9938 2.5020 -2.8 0026 .0008 -0.1 4602 3509 26 .9953 2.6015 -2.7 .0035 .0011 .0 .5000 3989 2.7 9965 2.7011 -2.6 .0047 .0015 .1 5398 .4509 2.8 .9974 2.8008 -2.5 0062 0020 2 .5793 5069 2.9 9981 2.9005 -2.4 0082 .0027 3 .6179 .5668 3.0 9987 3.0004 -2.3 0107 0037 4 .6554 .6304 3.1 .9990 3.1003 -22 0139 0049 5 .6915 .6978 3.2 9993 3.2002 -2.1 0179 .0065 6 .7257 .7687 33 9995 3.3001 -2.0 0228 0085 .7 .7580 8429 3.4 .9997 3.4001 -1.9 0287 8 .9202 3.5 9998 3.5001 0111 0143 -1.8 .9 .7881 8159 8413 0359 0446 .9998 3.6 3.7 -1.7 1.0 0183 0232 1.0004 1.0833 1.1686 1.2561 .9999 9999 0548 1.1 3.8 3.6000 3.7000 3.8000 3.9000 4.0000 -1.5 0293 1.2 8643 8849 9032 0668 0808 3.9 1.0000 1.0000 -1.4 .0367 1.3 1.3455 4.0