Graphs & greedy algorithms

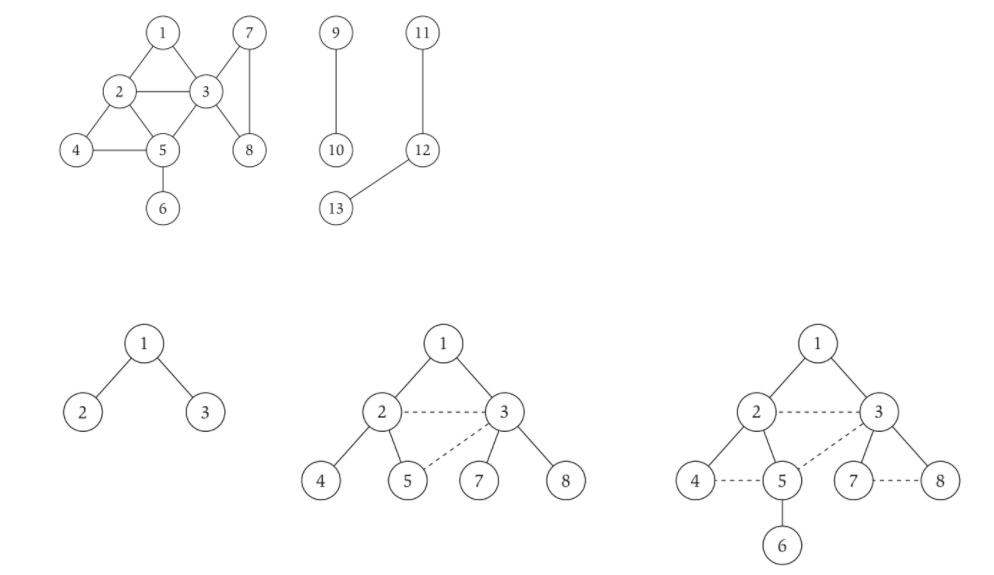
By modifying the breadth first search algorithm in 4.1 of L4 (note that we have a different problem here. A simple copy will not work.), write ONE algorithm in the format used in class to solve the following problem: Given a graph (V, E) and a starting node v, print the nodes of the graph in a breath first manner with respect to v: print v first, then all its neighbors that are not printed yet, then the neighbors (not printed) of the neighbors of v, and so on. 4. S-t connectivity problem Suppose we are given a graph G = (V, E) and two particular nodes s and t. We'd like to find an efficient algorithm that answers the question: Is there a path from s tot in G? We will call this the problem of determining s-t connectivity. 11 4 8 10 12 13 2 3 2 4 5 8 4 5 7 8 6 4.1 Breadth first search algorithm Example: 1-6 connectivity problem 1 2, 3 Algorithm (Function) Name: breadth Search Input G=(V, E) a graph S, starting node t, terminating node Output hasPath = true: there is a path from s tot = false otherwise Side effects N.A. Auxiliary data Q: a queue II a node in the queue means its neighbors need to be inspected // visited[i]: 0 means i is not visited, 1 otherwise Plan 1. put s into Q, and hasPath := false 2. while Q is not empty 3. take/remove the first element u from Q 4. if u ist 5. hasPath := true 6. break 7. else 8. mark u as visited 9. for each {u, v} \in E Il put the un-visited neighbors of u into Q 10. if v is not visited 11. put v into Q End of algorithm === 03/04/21 discussion about complexity of the algorithm === Observation: every node can but put into Q at most once Steps of for loop in line 9 is # of neighbors of node u (total steps: sum of the degree of every node) Step: 2*e (e is the number of edges of the graph) bigO(e) ===