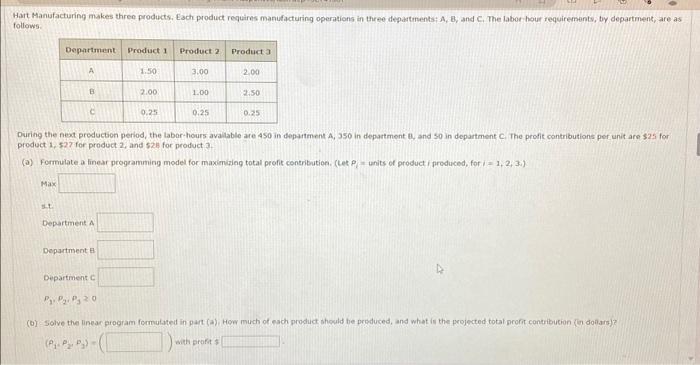
Hait Manufacturing makes three products. Each product requires manufacturing operations in three departments; A, B, and C. The labor hour requirements, by department, are as follows. During the next production period, the labor-hours avaliable are 450 in department A, 350 in department B, snd so in department C. The profit contributions per unit are 325 for product 1, 527 for product 2, and 528 for product ? (a) Formulate a finear programming model for maximizing total profic contribution. (Let Pf= units of product i produced, for i=1,2,3i ) Mas st. Department A Department B Departiment C P1,P2,P30 (b) Solve the linear program formulated in part (a). How much of each product should be produced, and what is the projected total profic contribution (in doiars)? (P1,P2,P2)=(withprofits (c) After evaluating the solution ottained in part (b), one of the production supervisors noted that production setup costs had not been taken into accoune. She noted that setup costs are $370 for product 1,$580 for product 2 , and $590 for peoduct 3 . If the solution developed in part (b) is to be used, what is the total profit contribution (in dollars) after taksing into account the setup costs? (d) Management realized that the optimal product mix, taking setup costs into account, might be different from the ene recommended in part (b). Formulate a mixed-integer linear program that takes setup costs into account. Management also sated that we should not copsider making more than 155 units of product 1 , 180 units of product 2 , or 190 units of product 3 . (Let Pf= units of product i produced and j be the 01 variable that is one if any quantity of product is produced and zero otherwise, for, 1,1,2,3. ) What is the objective function of the mixed-integer linear program? Max In addition to the constraints from part (a), what other constraints should be added to the mixed-integer finear program? s.t. units of Product 1 produced units of Product 2 produced units of product 3 produced 1,2,P20;Y1,Y2,Y0=0,1 (e) Solve the mixed-integer linear program formulated in part (d). How much of each product should be produced, and what is the peojected total profit (in dol brs) contritution? (e1,P2,P3,y1,y2,y2)=(withperfits: