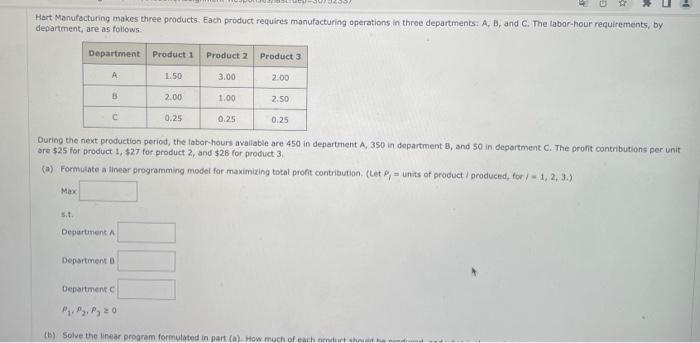
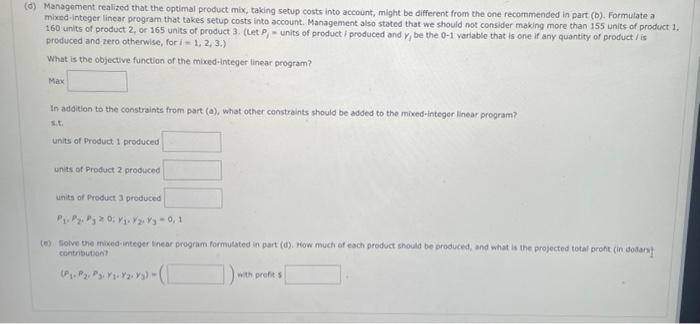
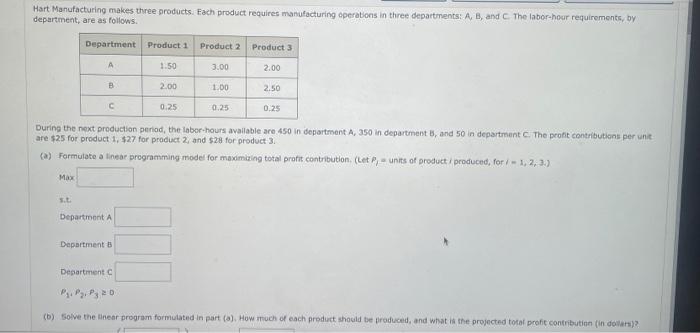
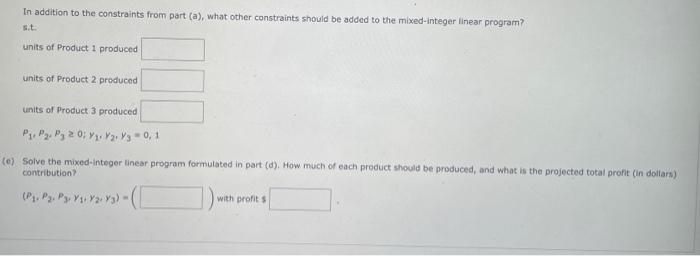
Hart Manufacturing makes three products. Each product requires manufacturing operations in three departments; A, B, and C. The labar-hour requirements, by department, are as foliows During the next production period, the labor-hours avaliable are 450 in department A,350 in dopartment B, and 50 in deportment C. The orofit contributions per unit bre $25 for product 1,$27 for product 2 , and $28 for product 3 . (a) Formulate a linear programming model for maximizing total pront contribution. (Let pj= units of product/ produced, for / = 1, 2, 3.) Max s.t. Department h Depsitiment 1 Denortment C p1,p2,p3=0 b) Solve the linear program formulated in part (a). How much of each product should be produced; and what is the projected total profit contribution (in doliars)? (P1,P2,P3)=(withprofit5 (c) After evaluating the solution obtained in part (b), one of the production supervisors noted that production setup costs had nat been taken into aceount. She noted that setup costs are $420 for product 1,$580 for product 2 , and $640 for product 3. If the solution developed in part (b) is to be used, what is the fotal profit contribution (in dallars) after taking into account the setup costs? (d) Management realized that the optimal product mix, taking setup costs into account, might be diflerent from the one recomnended in part (b). Formilate a mixed-integer linear program that takes setup costs into occount. Management also stated that we should not consider making more than is5 units of product 4 . 160 units of product 2 , or 165 units of product 3 . (Let , = units of product / produced and ybbethe01 variable that is one if any quantity of product / is produced and tero otherwise, for i=1,2,3. ) What is the objective function of the mixed-integer linear program? Max In adoition to the constraints from part (a). what other constraints should be sdded to the mixed-integer linear program? units of Product 1 produced units of Product 2 Droduced Units of Pioduct 2 produced 3) Management realized that the optimal product mix, taking setup costs into account, might be different from the one recornmended in part (b). Formulate a mixed-integer linear program that takes setup costs into account. Management also stated that we should not consider making more than 155 units of product 1. 160 units of product 2 , or 165 units of product 3 . (Let - = units of product i produced and y, be the 0 - 1 variable that is one if any quantity of product / is produced and zero otherwise, for i=1,2,3,) What is the objective function of the mixed integer linear program? Max In addition to the constraints from part (a), what other canstreints should be added to the mived-integer linear program? sit. units of Product 1 produced units of Product 2 proouced units of Product 3 produced P1,P2,P30,r1,V2,y3=0,1 (5) Golve the mixed-integer Dne or program formulated in part (d). Fow much of each product should be aroduced, and what is the projectod total aroht (in dodarn? contribution? (P1,P2,P3,Y1Y2,y3)=( Hart Manufacturing makes three groducts. Each product requires manufacturing operatons in three departments: A, B, and C. The labor-hour requirements, by department, are as follows. During the next production period, the Labor-hours available are 450 in department A, 350 in department B, and 50 in departrant C. The profi contributions per unit. are $25 for prodoct 1,$27 for product 2, and 528 for product 3 . (a) Formulate a Linear programming model for maximiting total profit contribution. (Let p,= units of groduct i produced, for 1 = 1 , 2, 3., ) Maxs.t.DepartmentADepartmentBDepartmentCP1,P2,P3=0 (b) Golve the Inear program formulated in part (a). How moch of each product shosid be froduced, and what if the projected totat profit contributinn (in doliats)? (b) Solve the innear program formulated in part (a). How much of each product should be produced, and what is the projected total profit contribution (in dollars)? (P1,P2,P3)=( with profit 5 (c) After evaluating the solution obtained in part (b), one of the production supervisors noted that production setup costs had nok been taken into account. She noted that setup costs are $420 for product 1, $580 for product 2 , and 5640 for product 3 . If the solution developed in part (b) is to be used, what is the total profit contribution (in doliars) after taking into account the setup costs? (a) Management realized that the optimat product mix, taking setup costs into account, might be different from the one recommended in part (b). Formulate a mixed-integer linear program that takes setup costs into account, Mansgement also stated that we should not consider making more than is5 units of product 1. 160 units of product 2 , or 165 units of product 3 . (Let Pj= units of product i produced and y, be the 0 - 1 variable that is one if any quanbity of product i is produced and zero otherwise, for 1=1,2,3. What is the objective function of the mixed-integer linear program? Max In addion to the constraints from part (a). What other constraints should be added to the mixed-integer inear program? s.t. units of Product 1 produced units of Product 2 produced In addition to the constraints from part (a), what other constraints should be added to the mixed-integer linear program? sit. units of Product 1 produced units of Product 2 produced units of Product 3 produced P1,P2,P30;y1,Y2,y3=0,1 (e) Solve the mixed-integer linear program formulated in part (d). How much of each procuct should be produced, and what is the projected total proft (in dollars) contribution? (P1,P2,P1,y1,y2,y3)=(withprofit3 Hart Manufacturing makes three products. Each product requires manufacturing operations in three departments; A, B, and C. The labar-hour requirements, by department, are as foliows During the next production period, the labor-hours avaliable are 450 in department A,350 in dopartment B, and 50 in deportment C. The orofit contributions per unit bre $25 for product 1,$27 for product 2 , and $28 for product 3 . (a) Formulate a linear programming model for maximizing total pront contribution. (Let pj= units of product/ produced, for / = 1, 2, 3.) Max s.t. Department h Depsitiment 1 Denortment C p1,p2,p3=0 b) Solve the linear program formulated in part (a). How much of each product should be produced; and what is the projected total profit contribution (in doliars)? (P1,P2,P3)=(withprofit5 (c) After evaluating the solution obtained in part (b), one of the production supervisors noted that production setup costs had nat been taken into aceount. She noted that setup costs are $420 for product 1,$580 for product 2 , and $640 for product 3. If the solution developed in part (b) is to be used, what is the fotal profit contribution (in dallars) after taking into account the setup costs? (d) Management realized that the optimal product mix, taking setup costs into account, might be diflerent from the one recomnended in part (b). Formilate a mixed-integer linear program that takes setup costs into occount. Management also stated that we should not consider making more than is5 units of product 4 . 160 units of product 2 , or 165 units of product 3 . (Let , = units of product / produced and ybbethe01 variable that is one if any quantity of product / is produced and tero otherwise, for i=1,2,3. ) What is the objective function of the mixed-integer linear program? Max In adoition to the constraints from part (a). what other constraints should be sdded to the mixed-integer linear program? units of Product 1 produced units of Product 2 Droduced Units of Pioduct 2 produced 3) Management realized that the optimal product mix, taking setup costs into account, might be different from the one recornmended in part (b). Formulate a mixed-integer linear program that takes setup costs into account. Management also stated that we should not consider making more than 155 units of product 1. 160 units of product 2 , or 165 units of product 3 . (Let - = units of product i produced and y, be the 0 - 1 variable that is one if any quantity of product / is produced and zero otherwise, for i=1,2,3,) What is the objective function of the mixed integer linear program? Max In addition to the constraints from part (a), what other canstreints should be added to the mived-integer linear program? sit. units of Product 1 produced units of Product 2 proouced units of Product 3 produced P1,P2,P30,r1,V2,y3=0,1 (5) Golve the mixed-integer Dne or program formulated in part (d). Fow much of each product should be aroduced, and what is the projectod total aroht (in dodarn? contribution? (P1,P2,P3,Y1Y2,y3)=( Hart Manufacturing makes three groducts. Each product requires manufacturing operatons in three departments: A, B, and C. The labor-hour requirements, by department, are as follows. During the next production period, the Labor-hours available are 450 in department A, 350 in department B, and 50 in departrant C. The profi contributions per unit. are $25 for prodoct 1,$27 for product 2, and 528 for product 3 . (a) Formulate a Linear programming model for maximiting total profit contribution. (Let p,= units of groduct i produced, for 1 = 1 , 2, 3., ) Maxs.t.DepartmentADepartmentBDepartmentCP1,P2,P3=0 (b) Golve the Inear program formulated in part (a). How moch of each product shosid be froduced, and what if the projected totat profit contributinn (in doliats)? (b) Solve the innear program formulated in part (a). How much of each product should be produced, and what is the projected total profit contribution (in dollars)? (P1,P2,P3)=( with profit 5 (c) After evaluating the solution obtained in part (b), one of the production supervisors noted that production setup costs had nok been taken into account. She noted that setup costs are $420 for product 1, $580 for product 2 , and 5640 for product 3 . If the solution developed in part (b) is to be used, what is the total profit contribution (in doliars) after taking into account the setup costs? (a) Management realized that the optimat product mix, taking setup costs into account, might be different from the one recommended in part (b). Formulate a mixed-integer linear program that takes setup costs into account, Mansgement also stated that we should not consider making more than is5 units of product 1. 160 units of product 2 , or 165 units of product 3 . (Let Pj= units of product i produced and y, be the 0 - 1 variable that is one if any quanbity of product i is produced and zero otherwise, for 1=1,2,3. What is the objective function of the mixed-integer linear program? Max In addion to the constraints from part (a). What other constraints should be added to the mixed-integer inear program? s.t. units of Product 1 produced units of Product 2 produced In addition to the constraints from part (a), what other constraints should be added to the mixed-integer linear program? sit. units of Product 1 produced units of Product 2 produced units of Product 3 produced P1,P2,P30;y1,Y2,y3=0,1 (e) Solve the mixed-integer linear program formulated in part (d). How much of each procuct should be produced, and what is the projected total proft (in dollars) contribution? (P1,P2,P1,y1,y2,y3)=(withprofit3