Answered step by step
Verified Expert Solution
Question
1 Approved Answer
H.E. Pennypacker, a wealthy American industrialist, is looking to purchase a silver mine in the mountains of Peru. In need of a loan, Pennypacker finances
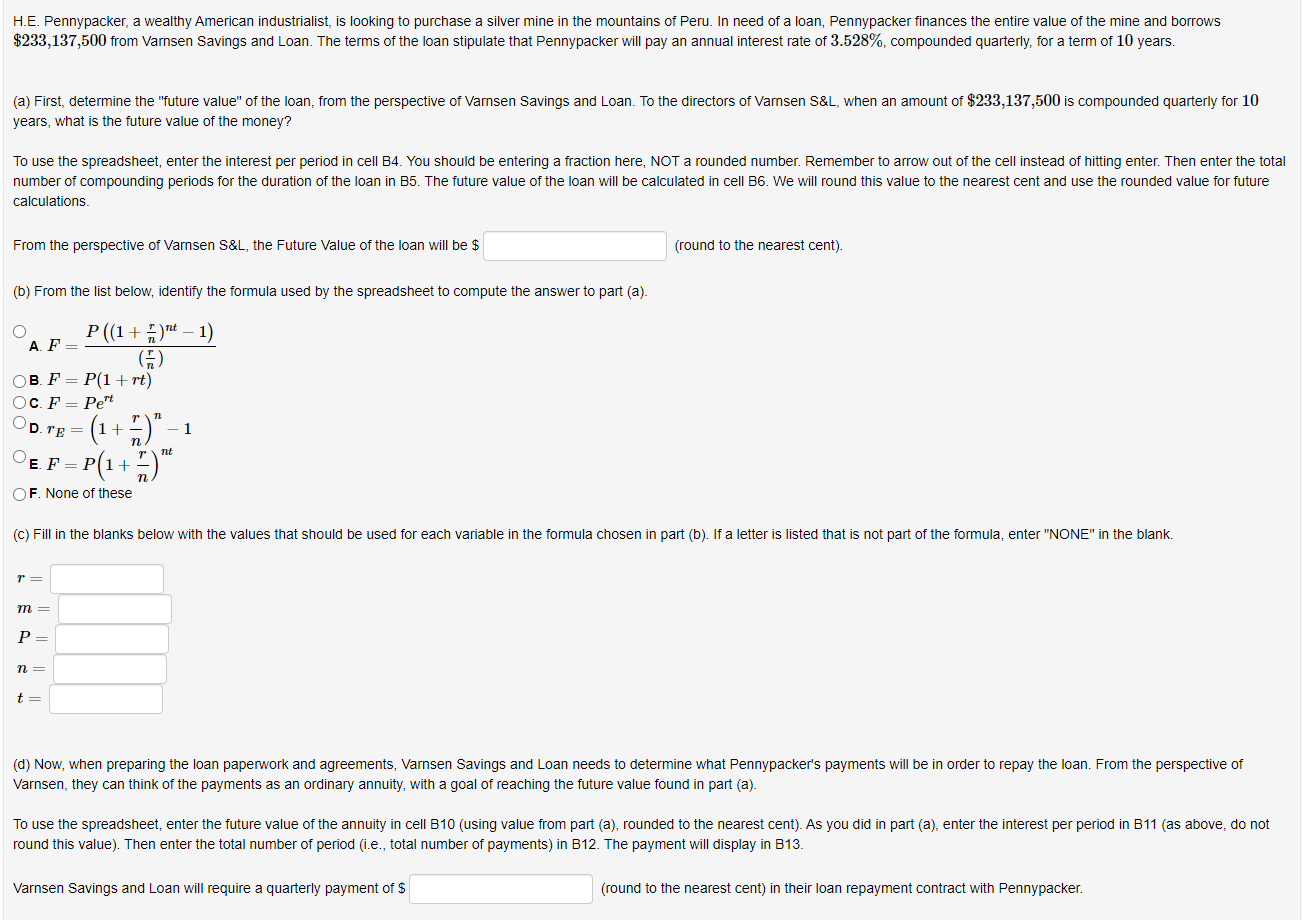
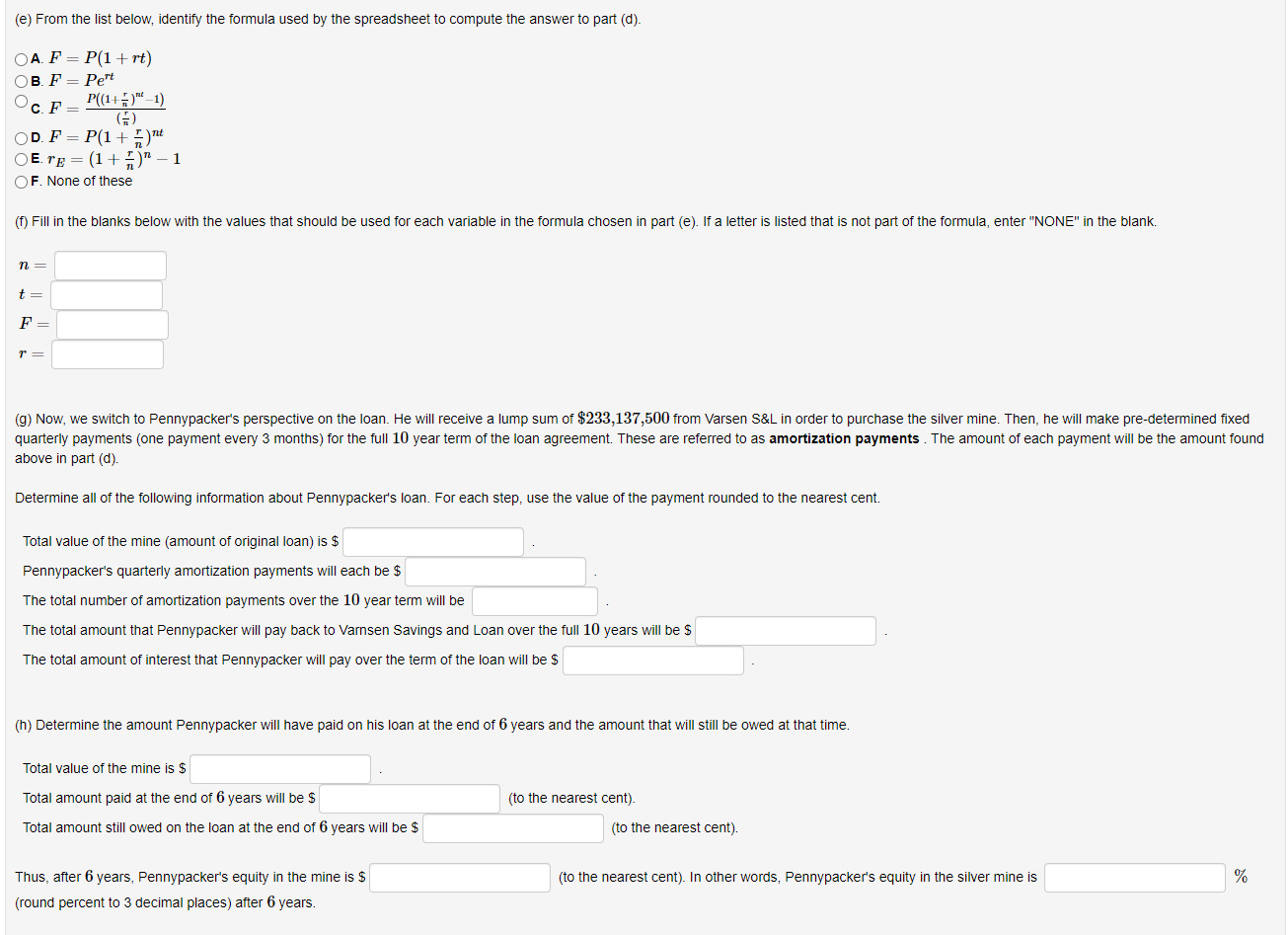
 H.E. Pennypacker, a wealthy American industrialist, is looking to purchase a silver mine in the mountains of Peru. In need of a loan, Pennypacker finances the entire value of the mine and borrows $233,137,500 from Varnsen Savings and Loan. The terms of the loan stipulate that Pennypacker will pay an annual interest rate of 3.528%, compounded quarterly, for a term of 10 years. (a) First, determine the "future value" of the loan, from the perspective of Varnsen Savings and Loan. To the directors of Varnsen S\&L, when an amount of $233,137,500 is compounded quarterly for 10 years, what is the future value of the money? To use the spreadsheet, enter the interest per period in cell B4. You should be entering a fraction here, NOT a rounded number. Remember to arrow out of the cell instead of hitting enter. Then enter the tota number of compounding periods for the duration of the loan in B5. The future value of the loan will be calculated in cell B6. We will round this value to the nearest cent and use the rounded value for future calculations. From the perspective of Varnsen S\&L, the Future Value of the loan will be $ (round to the nearest cent). (b) From the list below, identify the formula used by the spreadsheet to compute the answer to part (a). A. F=(nr)P((1+nr)nt1) B. F=P(1+rt) c. F=Pert D. rE=(1+nr)n1 =P(1+nr)nt F. None of these (c) Fill in the blanks below with the values that should be used for each variable in the formula chosen in part (b). If a letter is listed that is not part of the formula, enter "NONE" in the blank. r= m= P= n= t= (d) Now, when preparing the loan paperwork and agreements, Varnsen Savings and Loan needs to determine what Pennypacker's payments will be in order to repay the loan. From the perspective of Varnsen, they can think of the payments as an ordinary annuity, with a goal of reaching the future value found in part (a). To use the spreadsheet, enter the future value of the annuity in cell B10 (using value from part (a), rounded to the nearest cent). As you did in part (a), enter the interest per period in B11 (as above, do not round this value). Then enter the total number of period (i.e., total number of payments) in B12. The payment will display in B13. Varnsen Savings and Loan will require a quarterly payment of $ (round to the nearest cent) in their loan repayment contract with Pennypacker. (e) From the list below, identify the formula used by the spreadsheet to compute the answer to part (d). A. F=P(1+rt) B. F=Pert C. F=(nr)P((1+nr)tt1) D. F=P(1+nr)nt E. rE=(1+nr)n1 F. None of these (f) Fill in the blanks below with the values that should be used for each variable in the formula chosen in part (e). If a letter is listed that is not part of the formula, enter "NONE" in the blank. n= t= F= r= (g) Now, we switch to Pennypacker's perspective on the loan. He will receive a lump sum of $233,137,500 from Varsen S\&L in order to purchase the silver mine. Then, he will make pre-determined fixed quarterly payments (one payment every 3 months) for the full 10 year term of the loan agreement. These are referred to as amortization payments . The amount of each payment will be the amount found above in part (d). Determine all of the following information about Pennypacker's loan. For each step, use the value of the payment rounded to the nearest cent. Total value of the mine (amount of original loan) is $ Pennypacker's quarterly amortization payments will each be $ The total number of amortization payments over the 10 year term will be The total amount that Pennypacker will pay back to Varnsen Savings and Loan over the full 10 years will be $ The total amount of interest that Pennypacker will pay over the term of the loan will be $ (h) Determine the amount Pennypacker will have paid on his loan at the end of 6 years and the amount that will still be owed at that time. Total value of the mine is $ Total amount paid at the end of 6 years will be $ (to the nearest cent). Total amount still owed on the loan at the end of 6 years will be $ (to the nearest cent). Thus, after 6 years, Pennypacker's equity in the mine is $ (to the nearest cent). In other words, Pennypacker's equity in the silver mine is % (round percent to 3 decimal places) after 6 years. LoanAmount=P(nr1(1+nr)nt)$233,137,500=P(40.035281(1+40.03528)410) According to this calculation, Pennypacker's quarterly payment should be $ H.E. Pennypacker, a wealthy American industrialist, is looking to purchase a silver mine in the mountains of Peru. In need of a loan, Pennypacker finances the entire value of the mine and borrows $233,137,500 from Varnsen Savings and Loan. The terms of the loan stipulate that Pennypacker will pay an annual interest rate of 3.528%, compounded quarterly, for a term of 10 years. (a) First, determine the "future value" of the loan, from the perspective of Varnsen Savings and Loan. To the directors of Varnsen S\&L, when an amount of $233,137,500 is compounded quarterly for 10 years, what is the future value of the money? To use the spreadsheet, enter the interest per period in cell B4. You should be entering a fraction here, NOT a rounded number. Remember to arrow out of the cell instead of hitting enter. Then enter the tota number of compounding periods for the duration of the loan in B5. The future value of the loan will be calculated in cell B6. We will round this value to the nearest cent and use the rounded value for future calculations. From the perspective of Varnsen S\&L, the Future Value of the loan will be $ (round to the nearest cent). (b) From the list below, identify the formula used by the spreadsheet to compute the answer to part (a). A. F=(nr)P((1+nr)nt1) B. F=P(1+rt) c. F=Pert D. rE=(1+nr)n1 =P(1+nr)nt F. None of these (c) Fill in the blanks below with the values that should be used for each variable in the formula chosen in part (b). If a letter is listed that is not part of the formula, enter "NONE" in the blank. r= m= P= n= t= (d) Now, when preparing the loan paperwork and agreements, Varnsen Savings and Loan needs to determine what Pennypacker's payments will be in order to repay the loan. From the perspective of Varnsen, they can think of the payments as an ordinary annuity, with a goal of reaching the future value found in part (a). To use the spreadsheet, enter the future value of the annuity in cell B10 (using value from part (a), rounded to the nearest cent). As you did in part (a), enter the interest per period in B11 (as above, do not round this value). Then enter the total number of period (i.e., total number of payments) in B12. The payment will display in B13. Varnsen Savings and Loan will require a quarterly payment of $ (round to the nearest cent) in their loan repayment contract with Pennypacker. (e) From the list below, identify the formula used by the spreadsheet to compute the answer to part (d). A. F=P(1+rt) B. F=Pert C. F=(nr)P((1+nr)tt1) D. F=P(1+nr)nt E. rE=(1+nr)n1 F. None of these (f) Fill in the blanks below with the values that should be used for each variable in the formula chosen in part (e). If a letter is listed that is not part of the formula, enter "NONE" in the blank. n= t= F= r= (g) Now, we switch to Pennypacker's perspective on the loan. He will receive a lump sum of $233,137,500 from Varsen S\&L in order to purchase the silver mine. Then, he will make pre-determined fixed quarterly payments (one payment every 3 months) for the full 10 year term of the loan agreement. These are referred to as amortization payments . The amount of each payment will be the amount found above in part (d). Determine all of the following information about Pennypacker's loan. For each step, use the value of the payment rounded to the nearest cent. Total value of the mine (amount of original loan) is $ Pennypacker's quarterly amortization payments will each be $ The total number of amortization payments over the 10 year term will be The total amount that Pennypacker will pay back to Varnsen Savings and Loan over the full 10 years will be $ The total amount of interest that Pennypacker will pay over the term of the loan will be $ (h) Determine the amount Pennypacker will have paid on his loan at the end of 6 years and the amount that will still be owed at that time. Total value of the mine is $ Total amount paid at the end of 6 years will be $ (to the nearest cent). Total amount still owed on the loan at the end of 6 years will be $ (to the nearest cent). Thus, after 6 years, Pennypacker's equity in the mine is $ (to the nearest cent). In other words, Pennypacker's equity in the silver mine is % (round percent to 3 decimal places) after 6 years. LoanAmount=P(nr1(1+nr)nt)$233,137,500=P(40.035281(1+40.03528)410) According to this calculation, Pennypacker's quarterly payment should be $
H.E. Pennypacker, a wealthy American industrialist, is looking to purchase a silver mine in the mountains of Peru. In need of a loan, Pennypacker finances the entire value of the mine and borrows $233,137,500 from Varnsen Savings and Loan. The terms of the loan stipulate that Pennypacker will pay an annual interest rate of 3.528%, compounded quarterly, for a term of 10 years. (a) First, determine the "future value" of the loan, from the perspective of Varnsen Savings and Loan. To the directors of Varnsen S\&L, when an amount of $233,137,500 is compounded quarterly for 10 years, what is the future value of the money? To use the spreadsheet, enter the interest per period in cell B4. You should be entering a fraction here, NOT a rounded number. Remember to arrow out of the cell instead of hitting enter. Then enter the tota number of compounding periods for the duration of the loan in B5. The future value of the loan will be calculated in cell B6. We will round this value to the nearest cent and use the rounded value for future calculations. From the perspective of Varnsen S\&L, the Future Value of the loan will be $ (round to the nearest cent). (b) From the list below, identify the formula used by the spreadsheet to compute the answer to part (a). A. F=(nr)P((1+nr)nt1) B. F=P(1+rt) c. F=Pert D. rE=(1+nr)n1 =P(1+nr)nt F. None of these (c) Fill in the blanks below with the values that should be used for each variable in the formula chosen in part (b). If a letter is listed that is not part of the formula, enter "NONE" in the blank. r= m= P= n= t= (d) Now, when preparing the loan paperwork and agreements, Varnsen Savings and Loan needs to determine what Pennypacker's payments will be in order to repay the loan. From the perspective of Varnsen, they can think of the payments as an ordinary annuity, with a goal of reaching the future value found in part (a). To use the spreadsheet, enter the future value of the annuity in cell B10 (using value from part (a), rounded to the nearest cent). As you did in part (a), enter the interest per period in B11 (as above, do not round this value). Then enter the total number of period (i.e., total number of payments) in B12. The payment will display in B13. Varnsen Savings and Loan will require a quarterly payment of $ (round to the nearest cent) in their loan repayment contract with Pennypacker. (e) From the list below, identify the formula used by the spreadsheet to compute the answer to part (d). A. F=P(1+rt) B. F=Pert C. F=(nr)P((1+nr)tt1) D. F=P(1+nr)nt E. rE=(1+nr)n1 F. None of these (f) Fill in the blanks below with the values that should be used for each variable in the formula chosen in part (e). If a letter is listed that is not part of the formula, enter "NONE" in the blank. n= t= F= r= (g) Now, we switch to Pennypacker's perspective on the loan. He will receive a lump sum of $233,137,500 from Varsen S\&L in order to purchase the silver mine. Then, he will make pre-determined fixed quarterly payments (one payment every 3 months) for the full 10 year term of the loan agreement. These are referred to as amortization payments . The amount of each payment will be the amount found above in part (d). Determine all of the following information about Pennypacker's loan. For each step, use the value of the payment rounded to the nearest cent. Total value of the mine (amount of original loan) is $ Pennypacker's quarterly amortization payments will each be $ The total number of amortization payments over the 10 year term will be The total amount that Pennypacker will pay back to Varnsen Savings and Loan over the full 10 years will be $ The total amount of interest that Pennypacker will pay over the term of the loan will be $ (h) Determine the amount Pennypacker will have paid on his loan at the end of 6 years and the amount that will still be owed at that time. Total value of the mine is $ Total amount paid at the end of 6 years will be $ (to the nearest cent). Total amount still owed on the loan at the end of 6 years will be $ (to the nearest cent). Thus, after 6 years, Pennypacker's equity in the mine is $ (to the nearest cent). In other words, Pennypacker's equity in the silver mine is % (round percent to 3 decimal places) after 6 years. LoanAmount=P(nr1(1+nr)nt)$233,137,500=P(40.035281(1+40.03528)410) According to this calculation, Pennypacker's quarterly payment should be $ H.E. Pennypacker, a wealthy American industrialist, is looking to purchase a silver mine in the mountains of Peru. In need of a loan, Pennypacker finances the entire value of the mine and borrows $233,137,500 from Varnsen Savings and Loan. The terms of the loan stipulate that Pennypacker will pay an annual interest rate of 3.528%, compounded quarterly, for a term of 10 years. (a) First, determine the "future value" of the loan, from the perspective of Varnsen Savings and Loan. To the directors of Varnsen S\&L, when an amount of $233,137,500 is compounded quarterly for 10 years, what is the future value of the money? To use the spreadsheet, enter the interest per period in cell B4. You should be entering a fraction here, NOT a rounded number. Remember to arrow out of the cell instead of hitting enter. Then enter the tota number of compounding periods for the duration of the loan in B5. The future value of the loan will be calculated in cell B6. We will round this value to the nearest cent and use the rounded value for future calculations. From the perspective of Varnsen S\&L, the Future Value of the loan will be $ (round to the nearest cent). (b) From the list below, identify the formula used by the spreadsheet to compute the answer to part (a). A. F=(nr)P((1+nr)nt1) B. F=P(1+rt) c. F=Pert D. rE=(1+nr)n1 =P(1+nr)nt F. None of these (c) Fill in the blanks below with the values that should be used for each variable in the formula chosen in part (b). If a letter is listed that is not part of the formula, enter "NONE" in the blank. r= m= P= n= t= (d) Now, when preparing the loan paperwork and agreements, Varnsen Savings and Loan needs to determine what Pennypacker's payments will be in order to repay the loan. From the perspective of Varnsen, they can think of the payments as an ordinary annuity, with a goal of reaching the future value found in part (a). To use the spreadsheet, enter the future value of the annuity in cell B10 (using value from part (a), rounded to the nearest cent). As you did in part (a), enter the interest per period in B11 (as above, do not round this value). Then enter the total number of period (i.e., total number of payments) in B12. The payment will display in B13. Varnsen Savings and Loan will require a quarterly payment of $ (round to the nearest cent) in their loan repayment contract with Pennypacker. (e) From the list below, identify the formula used by the spreadsheet to compute the answer to part (d). A. F=P(1+rt) B. F=Pert C. F=(nr)P((1+nr)tt1) D. F=P(1+nr)nt E. rE=(1+nr)n1 F. None of these (f) Fill in the blanks below with the values that should be used for each variable in the formula chosen in part (e). If a letter is listed that is not part of the formula, enter "NONE" in the blank. n= t= F= r= (g) Now, we switch to Pennypacker's perspective on the loan. He will receive a lump sum of $233,137,500 from Varsen S\&L in order to purchase the silver mine. Then, he will make pre-determined fixed quarterly payments (one payment every 3 months) for the full 10 year term of the loan agreement. These are referred to as amortization payments . The amount of each payment will be the amount found above in part (d). Determine all of the following information about Pennypacker's loan. For each step, use the value of the payment rounded to the nearest cent. Total value of the mine (amount of original loan) is $ Pennypacker's quarterly amortization payments will each be $ The total number of amortization payments over the 10 year term will be The total amount that Pennypacker will pay back to Varnsen Savings and Loan over the full 10 years will be $ The total amount of interest that Pennypacker will pay over the term of the loan will be $ (h) Determine the amount Pennypacker will have paid on his loan at the end of 6 years and the amount that will still be owed at that time. Total value of the mine is $ Total amount paid at the end of 6 years will be $ (to the nearest cent). Total amount still owed on the loan at the end of 6 years will be $ (to the nearest cent). Thus, after 6 years, Pennypacker's equity in the mine is $ (to the nearest cent). In other words, Pennypacker's equity in the silver mine is % (round percent to 3 decimal places) after 6 years. LoanAmount=P(nr1(1+nr)nt)$233,137,500=P(40.035281(1+40.03528)410) According to this calculation, Pennypacker's quarterly payment should be $ Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


