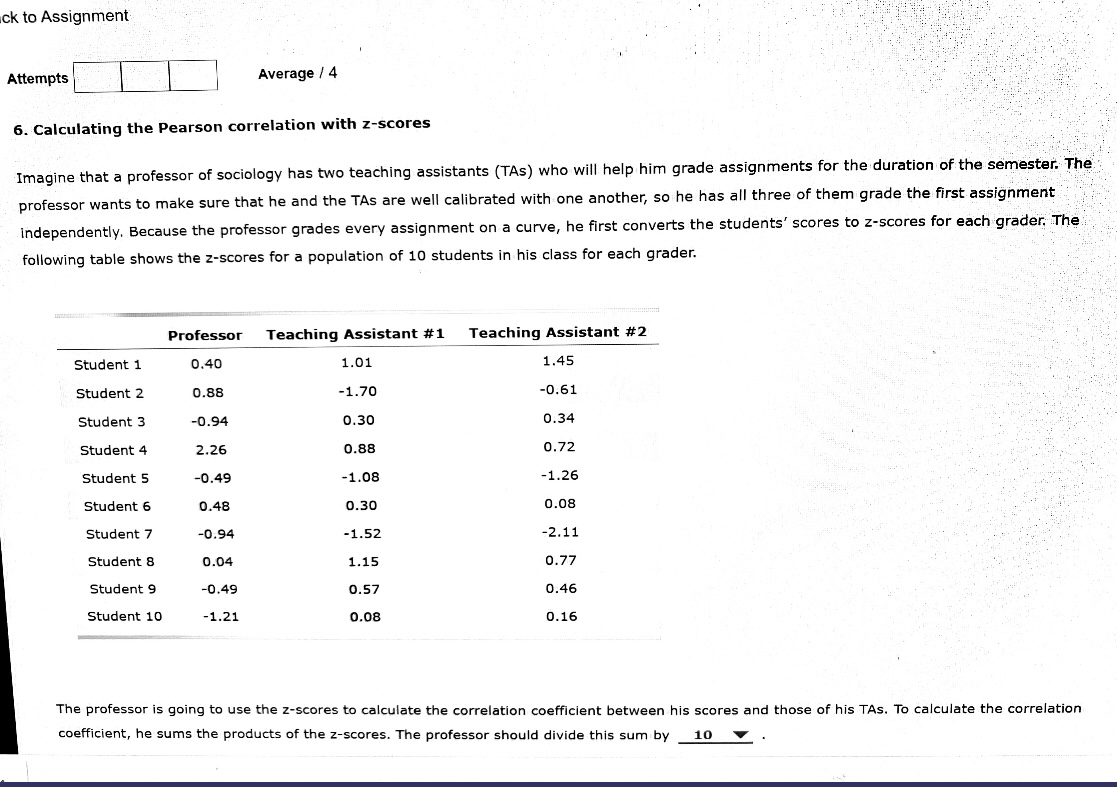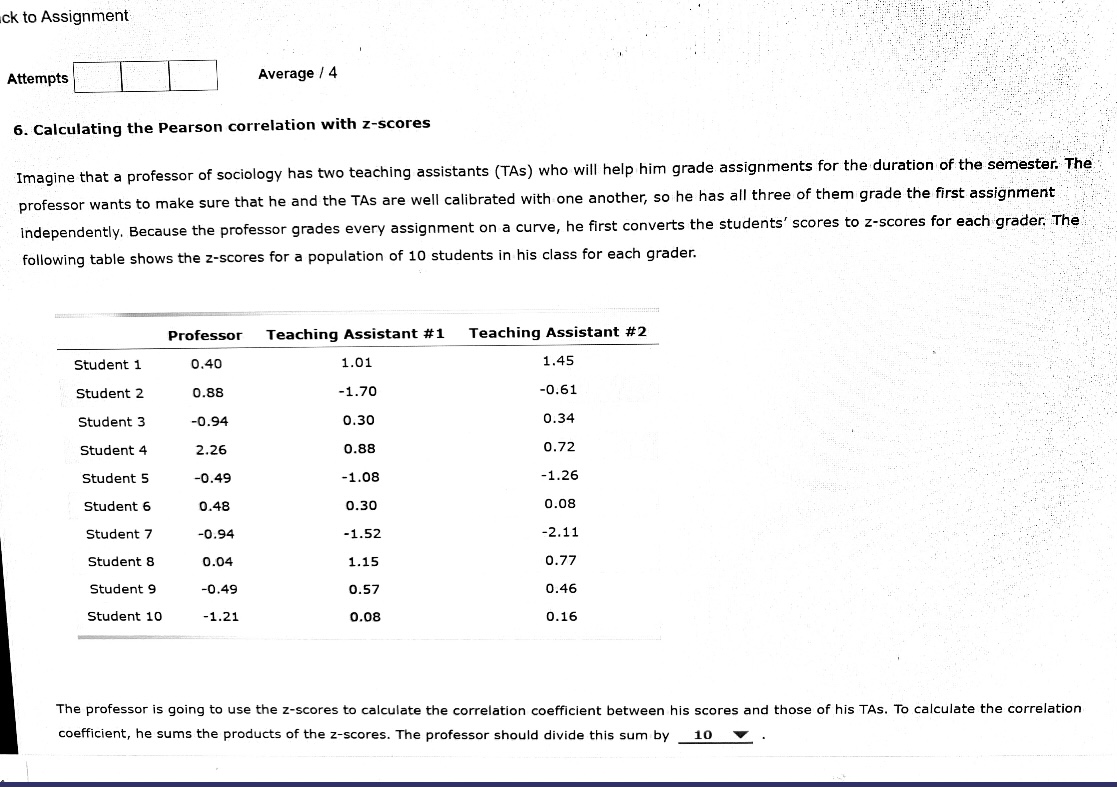
he professor is going to use the z-scores to calculate the correlation coefficient between his scores and those of his TAs. To calculate the correlation oefficient, he sums the products of the z-scores. The professor should divide this sum by _ 10 The professor constructed a table of correlation coefficients between his scores and those of his TAs. Select the correct missing correlation. Professor Teaching Assistant #1 Teaching Assistant #1 Teaching Assistant #2 0.36 0.90 Based on the correlation table, the professor should arrive at which of the following conclusions? The professor and both of his TAs are well calibrated. O The professor and TA #2 are well calibrated, but TA #1 is off. The two TAs are well calibrated with each other but not with the professor. O The professor and TA #1 are well calibrated, but TA #2 is off. The professor thinks he tends to be a harsh grader and decides to add 5 points to each student's grade before converting the scores to z-scores and computing the Pearson correlation coefficient between his grades and the two teaching assistants'. This change in the professor's scores will not change _ the correlation between the professor's scores and TA #1's and TA #2's scores. Grade It Now Save & Continue Continue without savingck to Assignment Attempts Average / 4 6. Calculating the Pearson correlation with z-scores Imagine that a professor of sociology has two teaching assistants (TAs) who will help him grade assignments for the duration of the semester. The professor wants to make sure that he and the TAs are well calibrated with one another, so he has all three of them grade the first assignment Independently. Because the professor grades every assignment on a curve, he first converts the students' scores to z-scores for each grader, The following table shows the z-scores for a population of 10 students in his class for each grader. Professor Teaching Assistant #1 Teaching Assistant #2 Student 1 0.40 1.01 1.45 Student 2 0.88 -1.70 -0.61 Student 3 -0.94 0.30 0.34 Student 4 2.26 0.88 0.72 Student 5 -0.49 -1.08 -1.26 Student 6 0.48 0.30 0.08 Student 7 -0.94 -1.52 -2.11 Student 8 0.04 1.15 0.77 Student 9 -0.49 0.57 0.46 Student 10 -1.21 0.08 0.16 The professor is going to use the z-scores to calculate the correlation coefficient between his scores and those of his TAs. To calculate the correlation coefficient, he sums the products of the z-scores. The professor should divide this sum by 10