Question
Heat treating is often used to carburize metal parts, such as gears. The thickness of the carburized layer is considered a crucial feature of the
Heat treating is often used to carburize metal parts, such as gears. The thickness of the carburized layer is
considered a crucial feature of the gear and contributes to the overall reliability of the part. Because of the
critical nature of this feature, two different lab tests are performed on each furnace load. One test is run on
a sample pin that accompanies each load. The other test is a destructive test, where an actual part is cross-
sectioned. This test involves running a carbon analysis on the surface of both the gear pitch (top of the gear
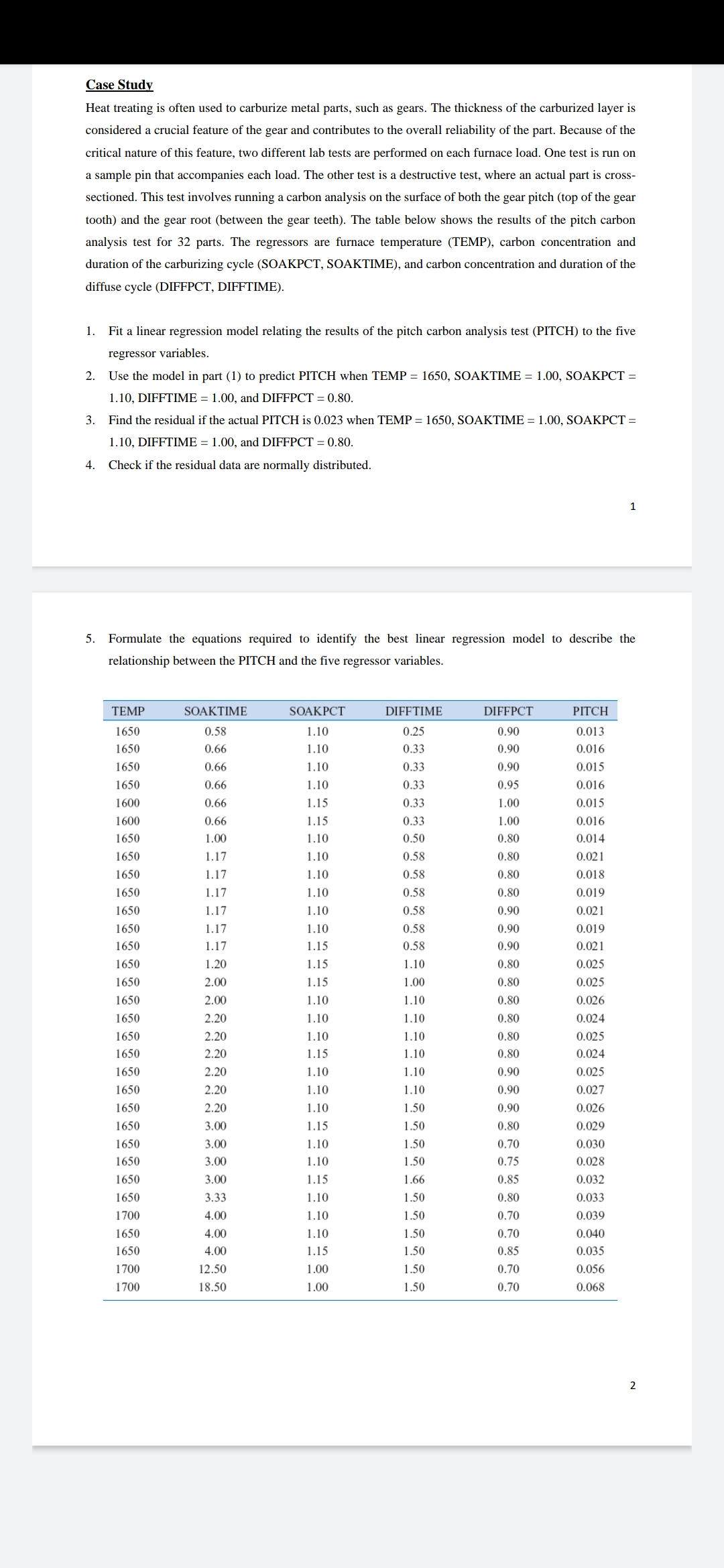
tooth) and the gear root (between the gear teeth). The table below shows the results of the pitch carbon
analysis test for 32 parts. The regressors are furnace temperature (TEMP), carbon concentration and
duration of the carburizing cycle (SOAKPCT, SOAKTIME), and carbon concentration and duration of the
diffuse cycle (DIFFPCT, DIFFTIME).
1. Fit a linear regression model relating the results of the pitch carbon analysis test (PITCH) to the five
regressor variables.
2. Use the model in part (1) to predict PITCH when TEMP = 1650, SOAKTIME = 1.00, SOAKPCT =
1.10, DIFFTIME = 1.00, and DIFFPCT = 0.80.
3. Find the residual if the actual PITCH is 0.023 when TEMP = 1650, SOAKTIME = 1.00, SOAKPCT =
1.10, DIFFTIME = 1.00, and DIFFPCT = 0.80.
4. Check if the residual data are normally distributed.
5. Formulate the equations required to identify the best linear regression model to describe
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


