Question
Hello, Appreciate if you can help me to find out the solution for the following problem. Denote by V(t) V ( t ) the replicating
Hello,
Appreciate if you can help me to find out the solution for the following problem.
Denote by V(t)V(t) the replicating portfolio of the payoff in problem number 4 (in this unit's practice problems and problem set) that does replication by investing the domestic currency in the foreign stock, the foreign bank account and the domestic bank account. Can you say, in terms of V(t)V(t), how much the replicating portfolio invests in each of these three assets, in each of the above two problems?
I am attaching the problem 4 of unit's practice problemsand its solution in UnitPracticeProblemAndSol.png
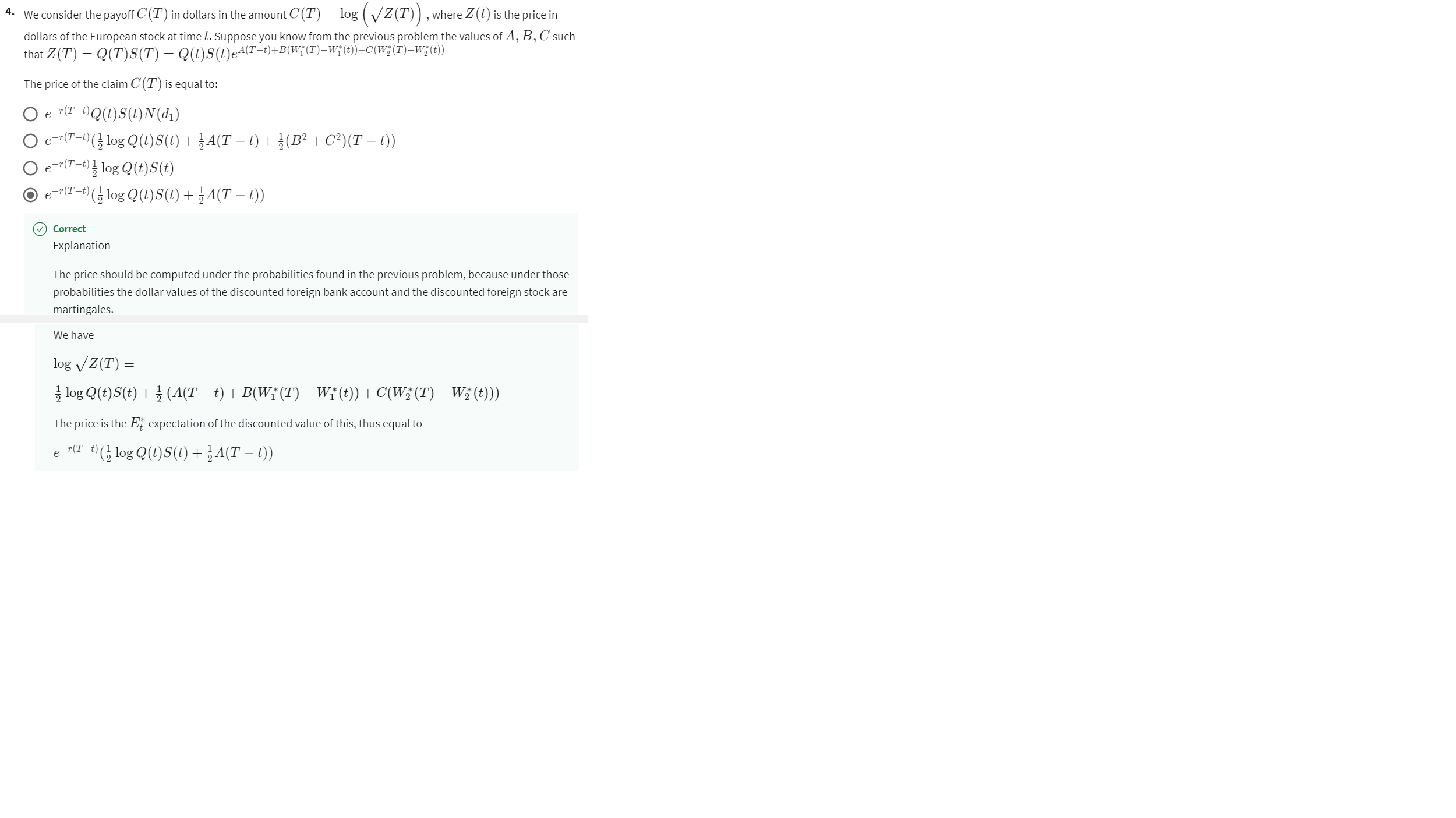
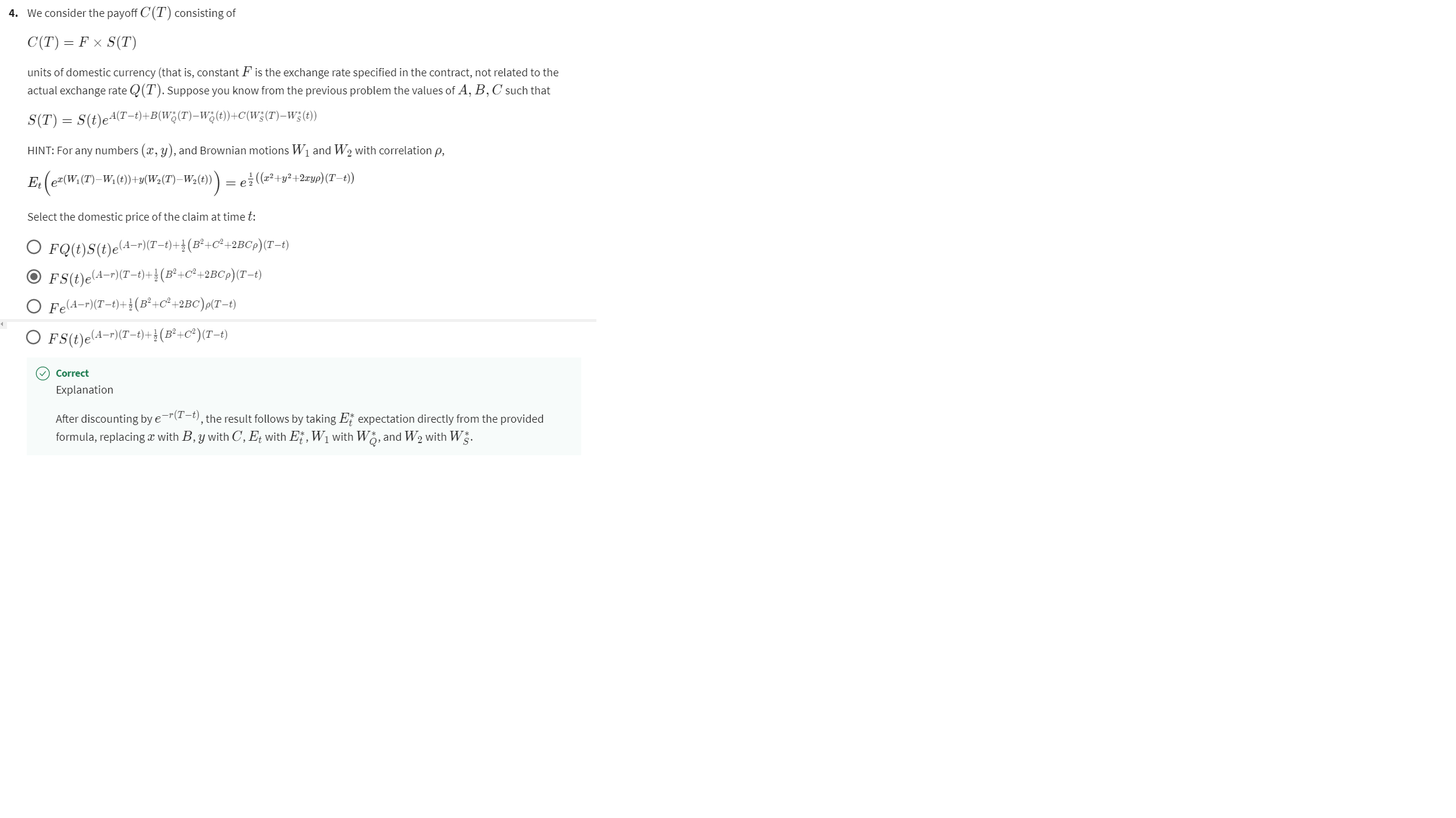
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


