Hello, I am having a very hard time with this question and am in need of help! Any questions or concerns please comment!

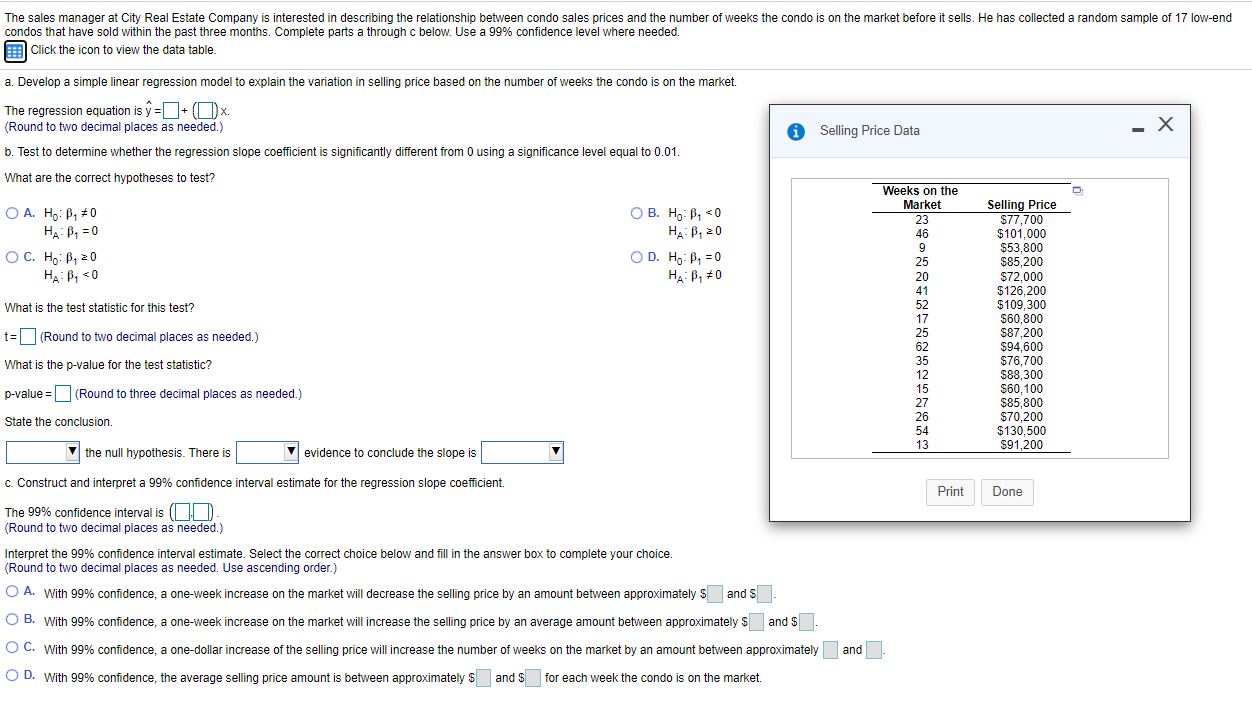
The sales manager at City Real Estate Company is interested in describing the relationship between condo sales prices and the number of weeks the condo is on the market before it sells. He has collected a random sample of 17 low-end condos that have sold within the past three months. Complete parts a through c below. Use a 99% confidence level where needed. Click the icon to view the data table. a. Develop a simple linear regression model to explain the variation in selling price based on the number of weeks the condo is on the market. The regression equation is y =+ (])x (Round to two decimal places as needed.) i Selling Price Data - X b. Test to determine whether the regression slope coefficient is significantly different from 0 using a significance level equal to 0.01. What are the correct hypotheses to test? Weeks on the Market O A. Ho: B, #0 OB. Ho B, =0 Selling Price 23 $77,700 HA : P1 =0 HA : B, 20 46 $101,000 9 $53,800 O C. Ho: B, 20 OD. Ho B, =0 25 $85,200 HA : P1 =0 HA : P, #0 20 $72,000 41 $126,200 What is the test statistic for this test? 52 $109,300 $60,800 1= (Round to two decimal places as needed.) 62 $87,200 $94,600 What is the p-value for the test statistic? 35 $76,700 12 $88,300 p-value = (Round to three decimal places as needed.) 15 $60, 100 27 $85,800 State the conclusion. 26 $70,200 $130,500 the null hypothesis. There is $91,200 evidence to conclude the slope is c. Construct and interpret a 99% confidence interval estimate for the regression slope coefficient. Print Done The 99% confidence interval is (][D) (Round to two decimal places as needed.) Interpret the 99% confidence interval estimate. Select the correct choice below and fill in the answer box to complete your choice. (Round to two decimal places as needed. Use ascending order.) O A. With 99% confidence, a one-week increase on the market will decrease the selling price by an amount between approximately $ and s O B. With 99% confidence, a one-week increase on the market will increase the selling price by an average amount between approximately $ and $ C. With 99% confidence, a one-dollar increase of the selling price will increase the number of weeks on the market by an amount between approximately and O D. With 99% confidence, the average selling price amount is between approximately $ and $ for each week the condo is on the market