Hello I have an algorithm question could you help me? You are working on techniques for coordinating groups of mobile robots. Each robot has a radio transmitter that it uses to communicate with a base station, and if robots gets too close to one another, then there are problems with interference among the transmitters. So a natural problem arises: how to plan the motion of the robots in such a way that each robot gets to its intended destination, but in the process the robots dont come close enough together to cause interference problems. You can model this problem as follows. Suppose that we have an undirected graph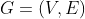, representing the floor plan of the building, and there are two robots initially located at nodes a and b in the graph. The robot at node a wants to travel to node c along a path in G, and the robot at node b wants to travel to node d. This is accomplished by means of a schedule: at each time step, the schedule specifies that exactly one of the robots move across a single edge, from one node to a neighboring node; at the end of the schedule, the robot from node a should be sitting on c, and the robot from b should be sitting on d. A schedule is interference-free if there is no point at which the two robots occupy nodes that are at a distance r from one another in the graph, for a given parameter r . Well assume that the two starting points a and b are at a distance greater than r , and so are the two ending nodes c and d. Q1)Give a polynomial-time algorithm that decides whether there exists an interference-free schedule by which each robot can get its destination. Q2)If your algorithm works in time 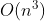, where 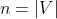, then you get additional 5 points. (Hint: A configuration for robots is an ordered pair (u, v), denoting the situation where the first robot is at node u, and the second node is at node v. Create a new graph H, where there is a corresponding node for every configuration (u, v) such that the distance between u and v is greater than r . Notice that you need to join two nodes of H by an edge if they represent configurations that could be consecutive in a schedule. You should be able to solve this problem, after this much hint.)

G (V. E) O(n3) G (V. E) O(n3)