Hello, I have this code that I need help with but no one has been able to respond.

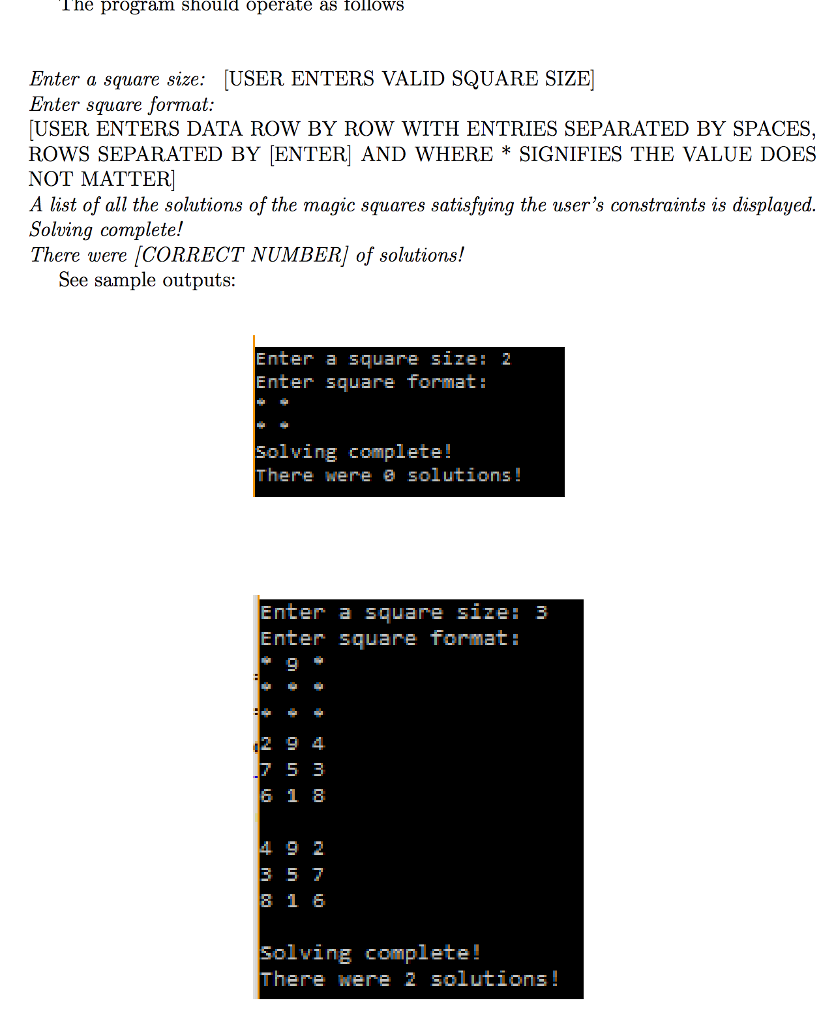
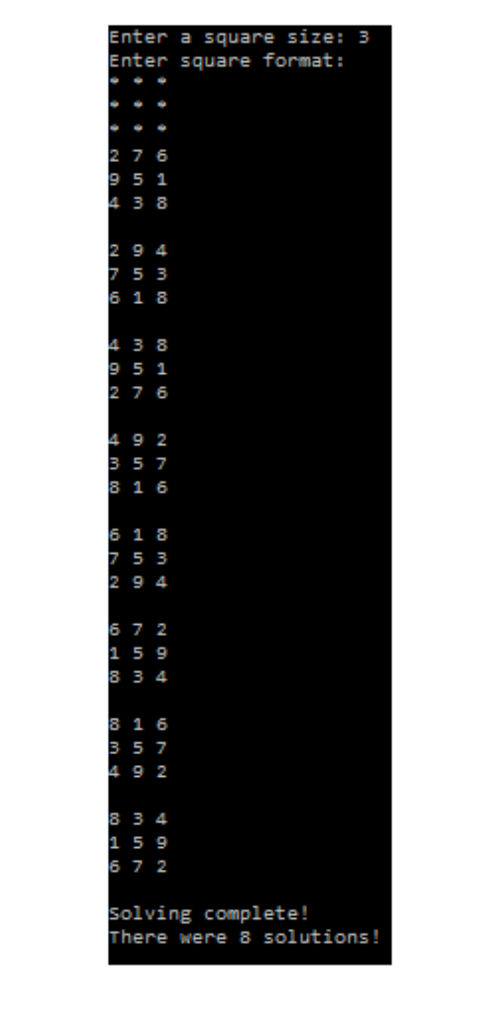
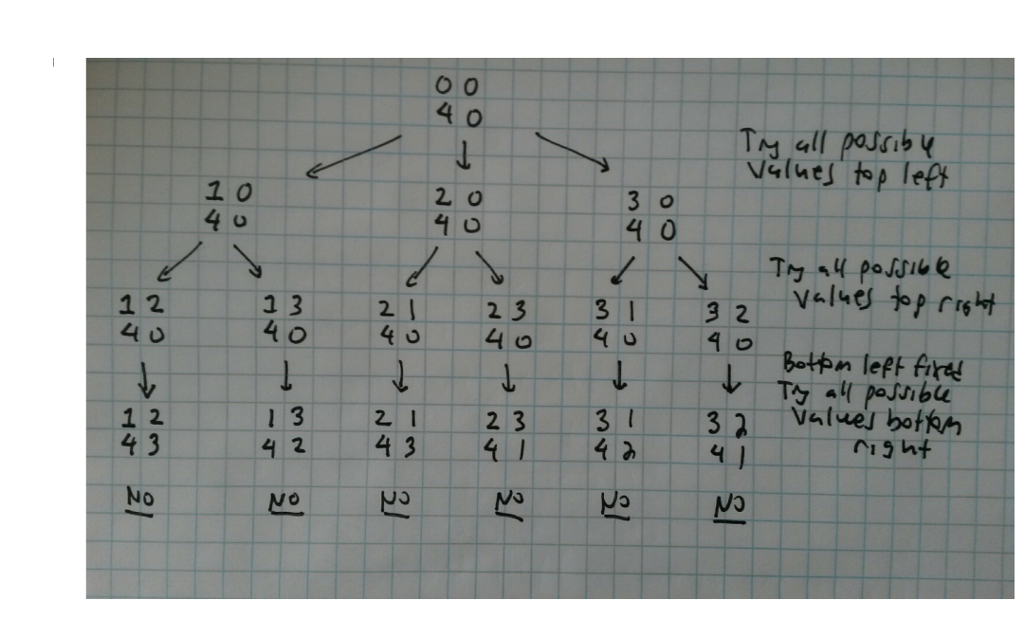
MAGIC SQUARE SOLVER A magic square is an n n array of the numbers 1 through n 2 such that each number only appears once, and the sum of every row, every column, and both main diagonals is the same. You might remember solving these back in elementary school: teachers would do this to keep the students busy... and quiet. Heres an example of one below: 4 9 2 3 5 7 8 1 6 Note that the sums for each row: 4 + 9 + 2, 3 + 5 + 7, 8 + 1 + 6 are all 15... as are the sums for each column: 4 + 3 + 8, 9 + 5 + 1, 2 + 7 + 6... as are the sums for both diagonals: 4 + 5 + 6, 2 + 5 + 8. In this homework, you will write the implementations to solve an n by n magic square where the user may, if they wish, enforce the placement of some numbers. You must use recursion in this assignment. This is the whole point of this exercise. Credit will not be given if you do not use recursion. 1 The program should operate as follows Enter a square size: [USER ENTERS VALID SQUARE SIZE] Enter square format: [USER ENTERS DATA ROW BY ROW WITH ENTRIES SEPARATED BY SPACES, ROWS SEPARATED BY [ENTER] AND WHERE * SIGNIFIES THE VALUE DOES NOT MATTER] A list of all the solutions of the magic squares satisfying the users constraints is displayed. Solving complete! There were [CORRECT NUMBER] of solutions! See sample outputs: 2 3 The magic square will be stored as a std::vector where 0 indicates no value has been placed in the slot at a given row and column yet (recall the valid numbers are from 1 to n 2 ). You must write: an overloaded operator>> to read from a stream into a std::vector that will properly process the users input; an overloaded operator with an output stream in the format demonstrated; a function counter that stores a local static variable to track the number of solutions found and which returns the value of its count; a function empty to check if a given position in the magic square is empty; a function taken to check if a given number is already used in the magic square; a function checkValid to check if a complete magic square satisfies the proper conditions to be a solution; and a recursive function solveSquare that accepts a std::vector and an index tracking the number of slots already considered in the recursion. Here is the gist of solving the problem recursively: suppose that we look at the slots, possibly placing values within them, left-to-right, top-to-bottom, and that we have been through num slots already. Then: if num is equal to the total number of slots, we should check if the magic square is a valid solution and if so, print it, and increase our count of valid solutions; if not, then we should determine if the slot is empty (recall the user could specify values, too!) and if it is empty, we should try every possible unused value in the current slot and try solving the magic square for each value we insert by repeating the process with num now num + 1; otherwise, we should skip over the current slot and try solving the magic square by looking at the next slot and replacing num by num + 1. The diagram below may help show you the logic in finding no solutions to the 2 2 magic square where the user has specified the bottom-left corner is to be 4.

Organize your code well and at the end of this work, submit .h and .cpp files that, when compiled and linked, will produce a program to solve a magic square. MAGIC SQUARE SOLVER. A magic square is an n x n array of the numbers 1 through n2 such that each number only appears once, and the sum of every row, every column, and both main diagonals is the same. You might remember solving these back in elementary school: teachers would do this to keep the students busy... and quiet. Here's an example of one below: 4 9 2 3 5 7 8 1 6 Note that the sums for each row: 4 9 2, 3 5 7, 8 1 6 are all 15... as are the sums for each column: 4 3 8, 9 5 1, 2 7 6... as are the sums for both diagonals: 4 5 6, 2 5 8. In this homework, you will write the implementations to solve an n by n magic square where the user may, if they wish, enforce the placement of some numbers. You must use recursion in this assignment. This is the whole point of this exercise. Credit will not be given if you do not use recursion