Hello, I just need some help finishing this MATLAB code. I think I've got everything down but how to actually write out the impulse response in a way that is usable by MATLAB.

(Also if it looks like the plots will work out in a way that will sufficiently answer the questions.)

Here is my code:

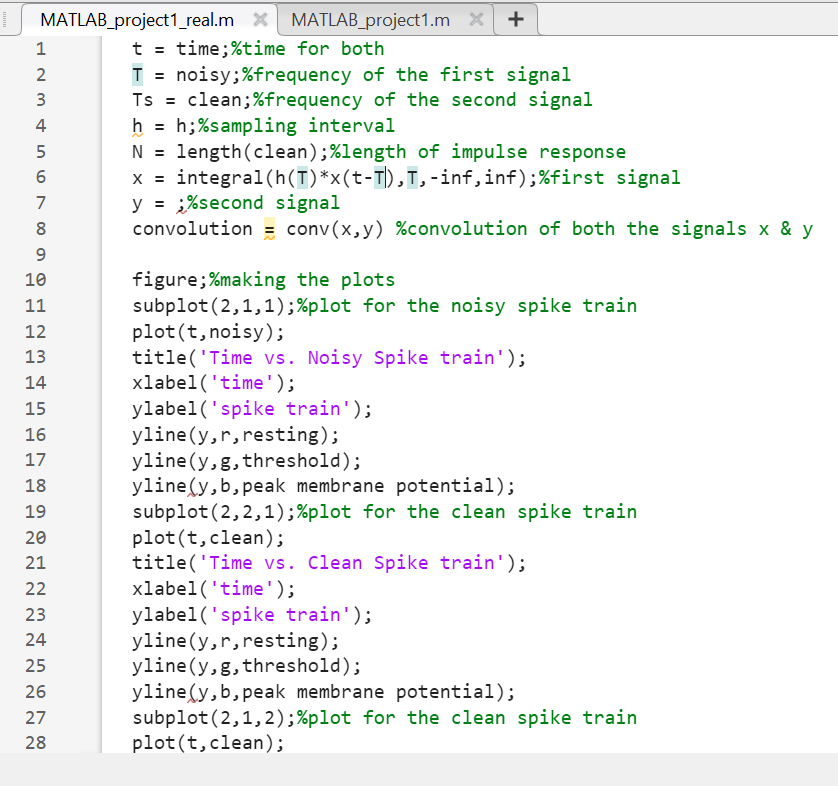
And here is the question in full:

Again, the things I need help with are making the "y(nTs)" equation into MATLAB format and an answer to the two questions "Does the code look like it will work?" and "Do the plots have everything the needed to answer a. and b.?"

Thank you very much!

28293031plot(t,clean);title("Timevs.ConvdSpiketrain");xlabel(time);ylabel("convdspiketrain"); Filtering a biological signal to remove noise: Action potentials (commonly referred to as spikes) are the electrical language that neurons use to communicate with one another. The first experiments to understand the mechanism of action potentials were performed on giant squid axons. These experiments involved stimulating the channels that control the movement of ions across the axon membrane with voltage pulses. The investigated ion channels were sodium, potassium and certain leak channels that allow the corresponding ions to flow in and out of the cell. A typical cell membrane has a negative resting membrane potential. When a voltage stimulus causes the axon to increase its membrane potential above a threshold, the sodium channels open causing an influx of sodium into the cell and depolarization to a peak potential (spiking). During this time, the potassium channels slowly open causing expulsion of potassium out of the cell and repolarization to the resting membrane potential. The resting, threshold, and peak membrane potentials are important parameters for characterizing axons. Measurement noise can be a practical problem in detecting these parameters. The file apdata.mat contains two computer-simulated giant squid axon action potential signals (spike trains) in units of mV and of 200 msec in duration with a "sampling interval" of 0.0796 msec each. One of the signals is artifact-free (vector labeled "clean"), while the other signal is contaminated with noise (vector labeled "noisy"). The file also includes the corresponding "time" vector for both signals (vector labeled "time"). The file apfilter.mat contains an impulse response for removing noise in the action potential signals while retaining information. The impulse response is given at the same sampling interval (vector labeled " h "). This discrete-time filter may be applied to originally continuous-time spike trains by approximating the convolution integral as follows: y(t)=h()x(t)dy(nTs)k=0N1h(kTs)x((nk)Ts)Ts where TS=0.0796msec and N is the impulse response length here. a. Plot the two spike trains versus time and label the resting, threshold, and peak membrane potentials for the clean signal. Can the same information be readily seen for the noisy signal? b. Apply the filter to both spike trains using the built-in conv function. Plot the two filtered signals versus time. The filtered signals are longer than the original signals and have some transients at the edges. What causes these edge effects and how should they be handled? c. Describe the results of the filtering. Can you now better label the resting, threshold, and peak membrane potentials for the noisy signal? Has all the noise been removed from the noisy signal? d. What are the capabilities and limitations of filtering with an LTI system? Deliverables: Submit a single pdf file containing answers to the questions, properly labeled plots, and the source code