Hello I need help with my study guide. (Figures for each question are provided at the end of the page)

1.

(03.04 MC)

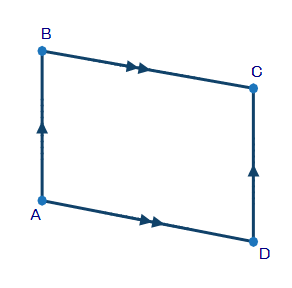
The following is an incomplete paragraph proving that the opposite sides of parallelogram ABCD are congruent:

According to the given information,and. Construct diagonal A C with a straightedge. _____________. Angles BAC and DCA are congruent by the Alternate Interior Angles Theorem. Angles BCA and DAC are congruent by the same theorem. Triangles BCA and DAC are congruent according to the Angle-Side-Angle (ASA) Theorem. By CPCTC, opposite sides AB and CD, as well as sides BC and DA, are congruent.

Which sentence accurately completes the proof? (5 points)

1.Angles BAC and DCA are congruent by the Same-Side Interior Angles Theorem.

2.Diagonal BD is congruent to itself by the Reflexive Property of Equality

3.Diagonal AC is congruent to itself by the Reflexive Property of Equality.

4.Angles ABC and CDA are congruent according to a property of parallelograms (opposite angles congruent).

2.(03.04 MC)

The following is an incomplete paragraph proving that the opposite angles of parallelogram ABCD are congruent:

According to the given information,and. Using a straightedge, extend segment AB and place point P above point B. By the same reasoning, extend segment AD and place point T to the left of point A. Angles BCD and PBC are congruent by the Alternate Interior Angles Theorem. Angles PBC and BAD are congruent by the ____________. By the Transitive Property of Equality, angles BCD and BAD are congruent. Angles ABC and BAT are congruent by the _____________. Angles BAT and CDA are congruent by the Corresponding Angles Theorem. By the Transitive Property of Equality,?ABC is congruent to?CDA. Consequently, opposite angles of parallelogram ABCD are congruent.

What theorems accurately complete the proof? (5 points)

1. Corresponding Angles Theorem/ Alternate Interior Angles Theorem

2. Alternate Interior Angles Theorem/ Corresponding Angles Theorem

3. Corresponding Angles Theorem/ Corresponding Angles Theorem

4. Alternate Interior Angles Theorem/ Alternate Interior Angles Theorem

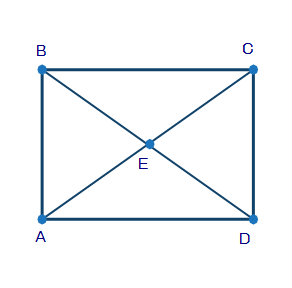
3.(03.04 MC)

The figure below shows rectangle ABCD:

The following two-column proof with missing statement proves that the diagonals of the rectangle bisect each other:

StatementReasonABCD is a rectangle.Givenandare parallelDefinition of a Parallelogramandare parallelDefinition of a Parallelogram?CAD ??ACBAlternate interior angles theoremDefinition of a ParallelogramAlternate interior angles theorem?? ADE ??? CBEAngle-Side-Angle (ASA) PostulateCPCTCCPCTCbisectsDefinition of a bisector

Which statement can be used to fill in the blank space? (5 points)

1.?ADB ??CBD

2.?ABE ??ADE

3.?ACD ??ACE

4.?ACE ??CBD

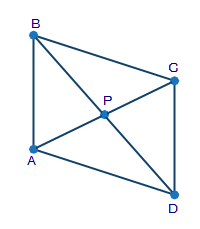
4.(03.04 MC)

In quadrilateral ABCD, diagonals AC and BD bisect one another:

What statement is used to prove that quadrilateral ABCD is a parallelogram? (5 points)

1.Segment AP is congruent to segment CP.

2.Segment BP is congruent to segment AP

3.Sides AB and BC are congruent.

4.Triangles BCP and CDP are congruent.

Figure for question 1.

\f\f\f