Hello Tutor!

Please help me on this homework assignment asap. Please indicate which question you are answering, write it on a sheet of paper (please don't type it out) for each question. If possible, make it into a single document and send all the questions together on paper.

Please note these question i need a lot of help with:

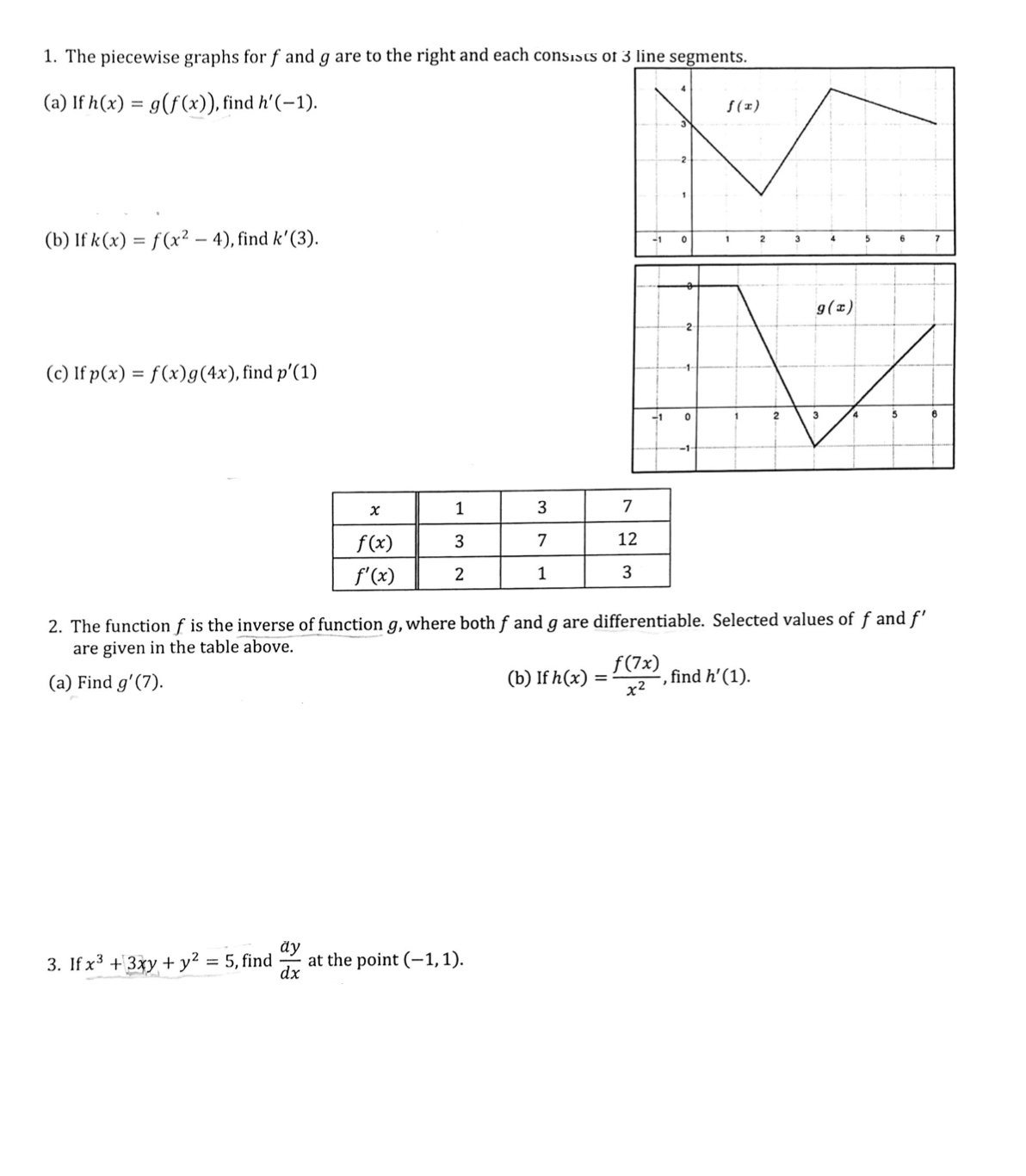
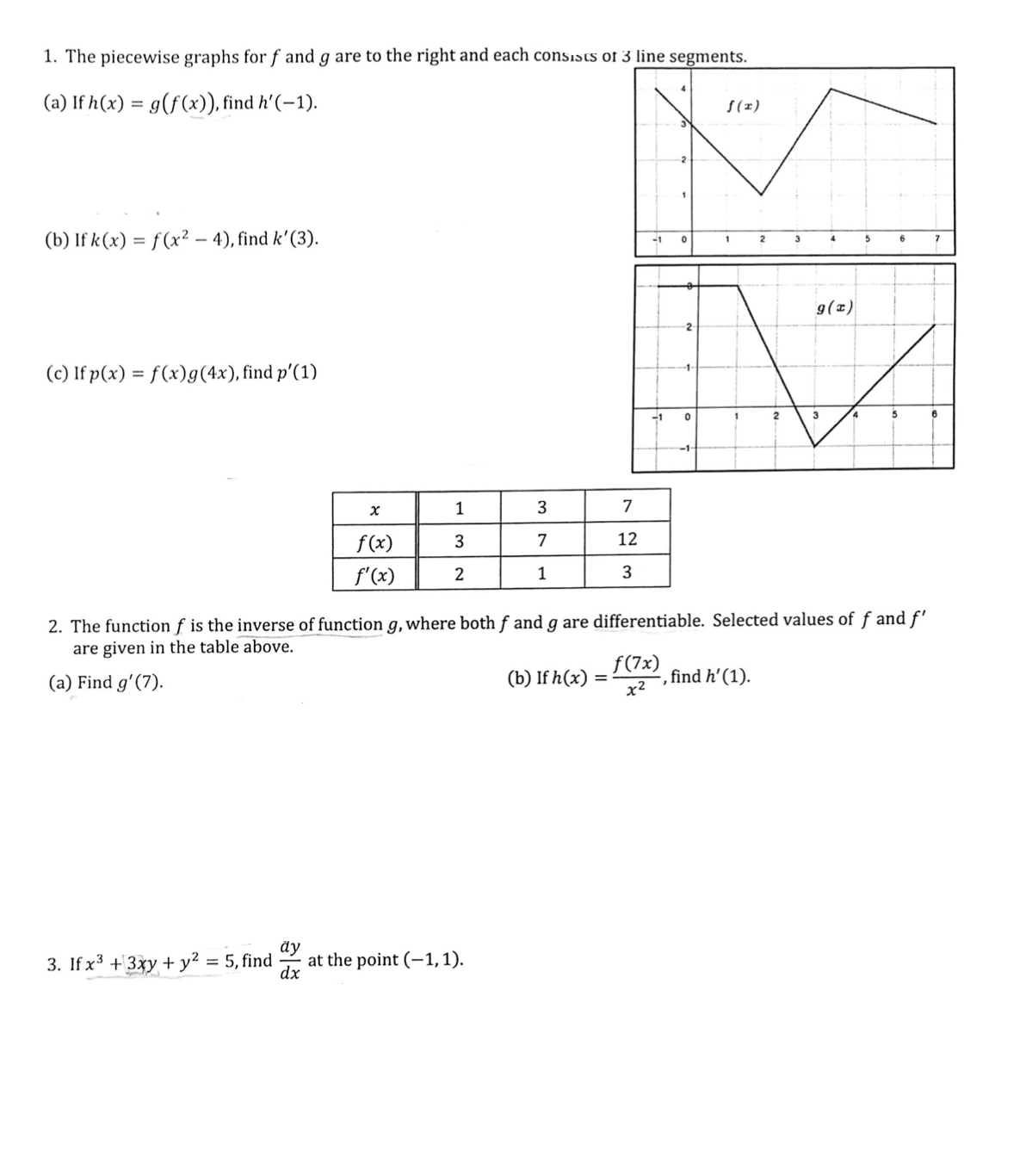
1. Question #1 (Part B): Use chain rule and graph to answer. Please show all work clearly and neatly (:

2. Question #2 (Part A): I need to find derivative on inverse (1/f'(3) = 0?) Please also work to get to the final answer.

3. Question #5: I got this problem very confused and I am not sure how to solve it. Please help and show all work. Include units!

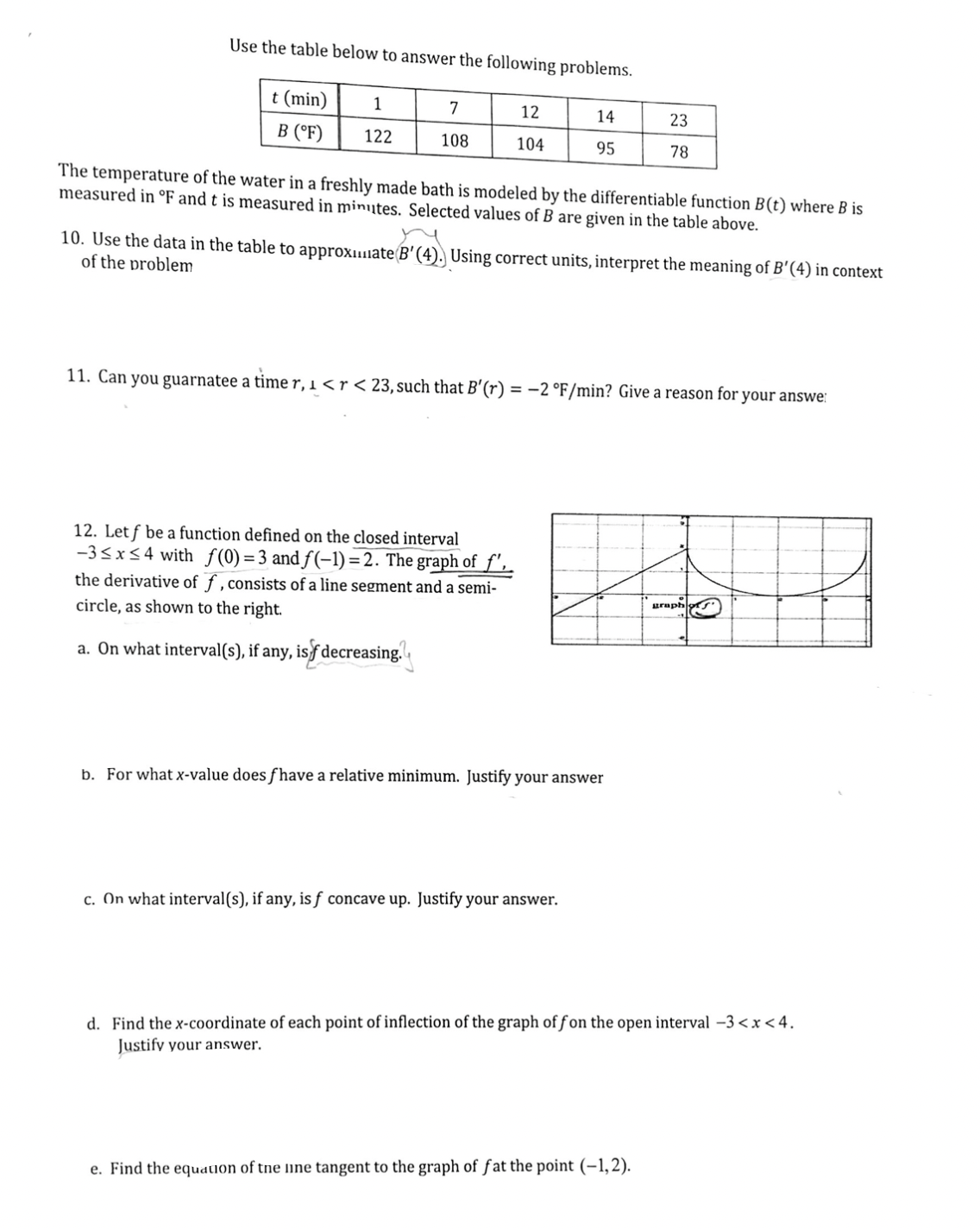
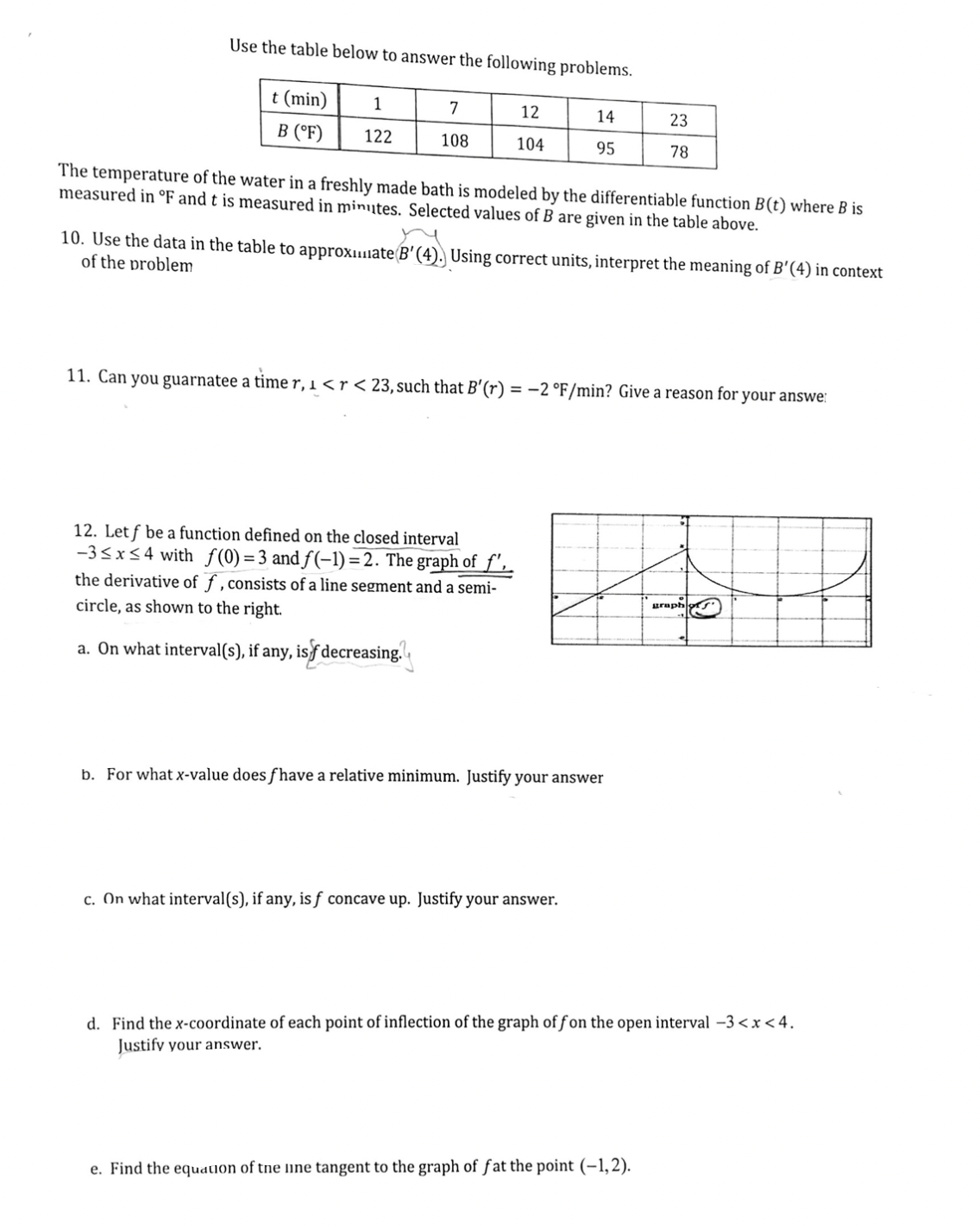
4. Question #8: USE EVT: Please provide all points tested by EVT and Justify answer with explanation.

5. Question #9: Show all work, include equations use, derivatives, and how to find length, & width.

6. #10: Show all work, include equations use, derivatives, and how to find length, & width. PLEASE INCLUDE UNITS!

7. #11: Please provide thorough calculus explanation

8. 12: Part B, C, D: Justify answer and show all work.

I would appreciate it so much so I can get a better understanding. Please provide through explanations and work for all questions. Please note these question request above. Thank you so much! I truly appreciate the support! (:

1. The piecewise graphs for f and g are to the right and each consists of 3 line segments. (a) If h(x) = g(f(x)), find h'(-1). S (z) (b) If k(x) = f(x2 - 4), find k' (3). 1 2 9 (z) (c) If p(x) = f(x)g(4x), find p'(1) 1 3 7 f (x) 3 12 f' (x) 2 1 3 2. The function f is the inverse of function g, where both f and g are differentiable. Selected values of f and f' are given in the table above. (a) Find g'(7). (b) If h(x) = (7x) x2 , find h' (1). 3. If x3 + 3xy + y2 = 5, find at the point (-1, 1).4. A particle moves along the x axis with position (t) = t2 - 2t - 8. Find the time t when the velocity of the particle is 9. 5. The area of a circle is decreasing at a rate of 4 cm2/sec. Find the rate that the radius is changing when the area of the circle is 367 cm . 6. The function f(x) = cos(x) + 5x - 3 has a tangent line at x = 0. Use this tangent line to approximate f (0.1). sin (1 - x2) 7. lim - x-1 e2x-2 - x 8. Let f(x) = 4x2 + 8x - 4, Find the minimum and maximum values for f (x) on the interval [-3, 2]. Justify your answer. 9. A rectangular area is to be fenced in using two types of fencing. The front and back uses fencing costing $5 a foot while the sides use fencing costing $4 a foot. If the area of the rectangle must contain 500 square feet, what should be the dimensions of the rectangle in order to keep the cost to a minimumUse the table below to answer the following problems. t (min) 7 12 14 23 B (OF) 122 108 104 95 78 The temperature of the water in a freshly made bath is modeled by the differentiable function B(t) where B is measured in OF and t is measured in minutes. Selected values of B are given in the table above. 10. Use the data in the table to approximate B'(4). Using correct units, interpret the meaning of B'(4) in context of the problem 11. Can you guarnatee a timer, 1