Help me answer these questions

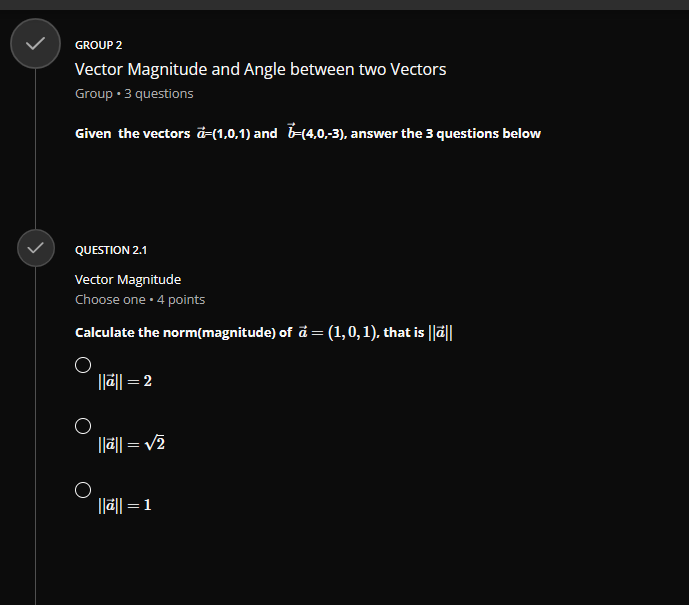
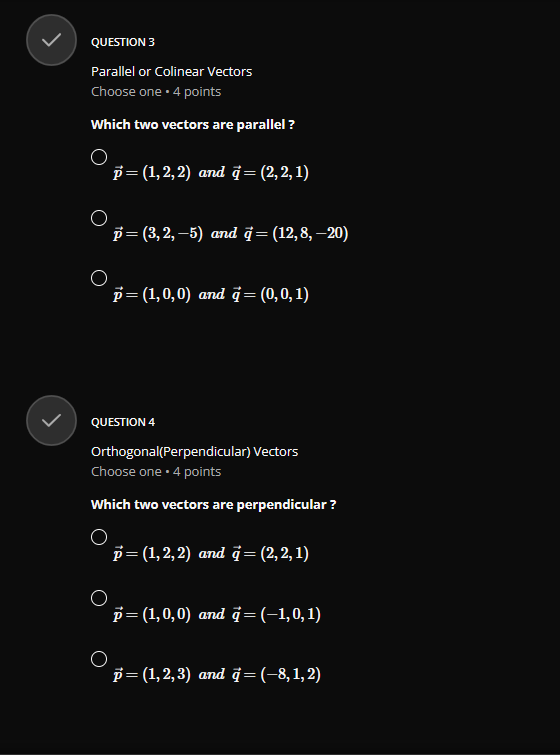
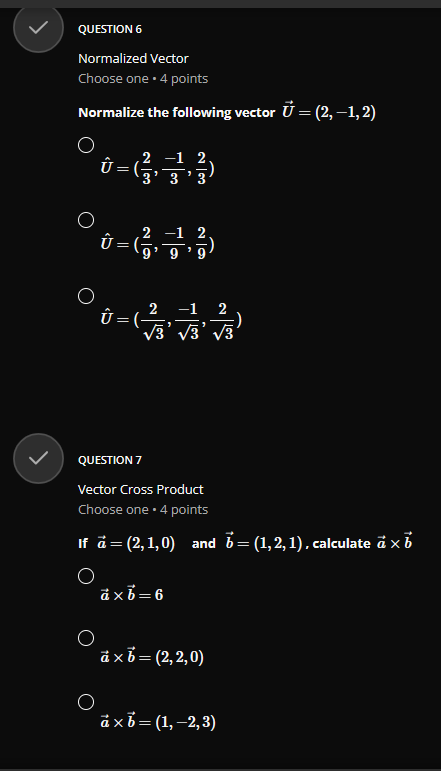
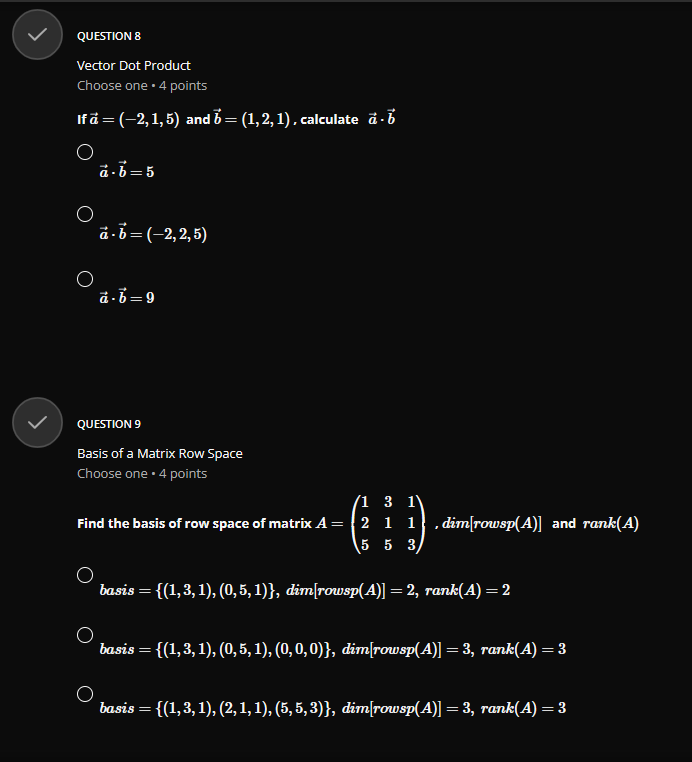
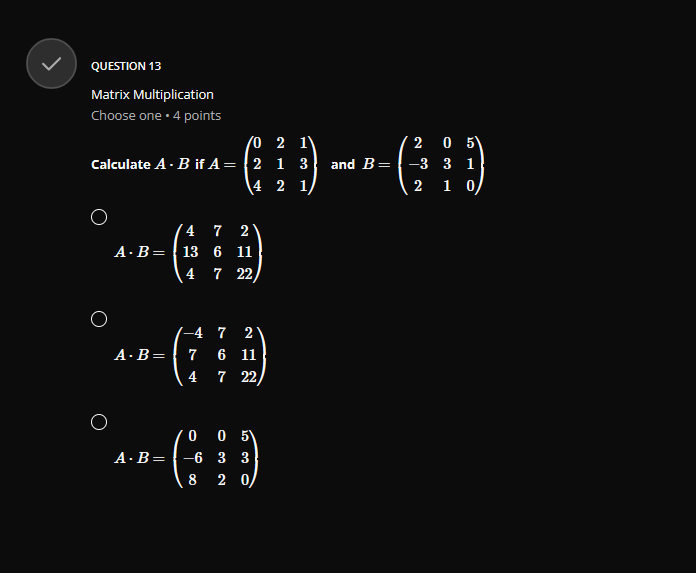
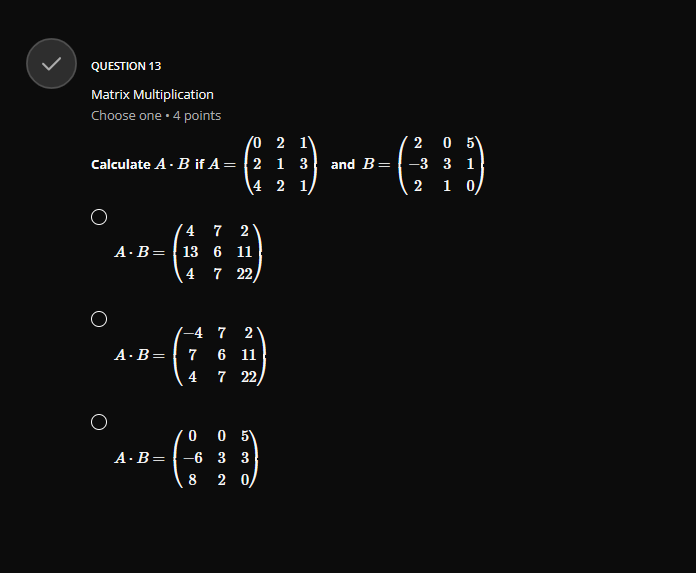
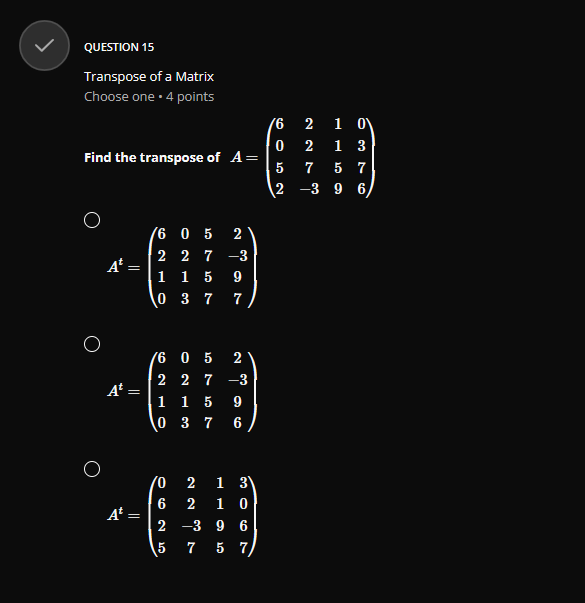
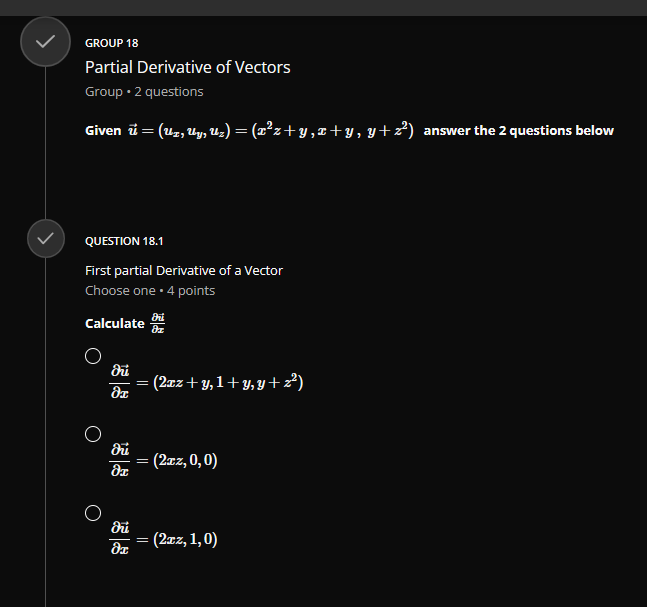
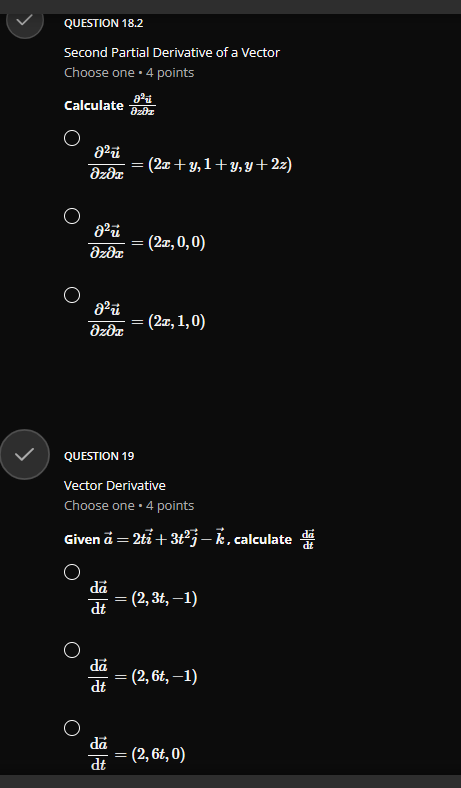
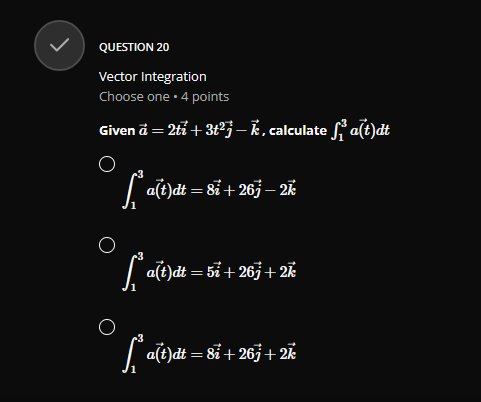
QUESTION 1 Vector Addition Choose one . 4 points Given the following vectors a = (-3, 2, 1) and b = (4, -2,3). calculate 2a -3b O 2a - 3b = (18, 10, -7) O 2a - 3b = (-18, 10, 7) O 2a - 3b = (-18, 10, -7)GROUP 2 Vector Magnitude and Angle between two Vectors Group . 3 questions Given the vectors a=(1,0,1) and b-(4,0,-3), answer the 3 questions below QUESTION 2.1 Vector Magnitude Choose one . 4 points Calculate the norm(magnitude) of a = (1, 0, 1), that is | |all O Ilall = 2 O llall = V2 O Hall = 1QUESTION 2.2 Vector magnitude Choose one . 4 points Calculate the norm(magnitude) of b = (4, 0, -3). that is | |3/| O 113 = 1 O 113/1 = V7 O 11611 = 5 QUESTION 2.3 Angle Between two Vectors Choose one . 4 points Calculate the angle 0 between the vectors a = (1, 0, 1) and b = (4, 0, -3) use a . b = a| . b | - cos(@) O 0 = 84.260 O 8 = 81.870 O 8 = 600QUESTION 3 Parallel or Colinear Vectors Choose one . 4 points Which two vectors are parallel ? p = (1, 2, 2) and q = (2, 2, 1) O p = (3, 2, -5) and q = (12, 8, -20) O p= (1, 0,0) and q = (0, 0, 1) QUESTION 4 Orthogonal(Perpendicular) Vectors Choose one . 4 points Which two vectors are perpendicular ? p = (1, 2,2) and q = (2, 2, 1) O p = (1,0,0) and q = (-1, 0, 1) O p = (1,2,3) and q = (-8, 1, 2)V QUESTION 5 Component and Projection of Vector Choose one . 4 points Given u = 2i + j -k = (2, 1, -1) and v = i + 27 + 2k = (1, 2,2) calculate: proj= = comp . i Remember : comp". = 4.U and v = - U , normalized vector of O H = (2, 4, 4) proj= = O 2 4 proj= = 81 81 81 O 2 4 4 pro]- = 9'9QUESTION 6 Normalized Vector Choose one . 4 points Normalize the following vector U = (2, -1, 2) C U = 3 C 1 9 O 2 3 3 QUESTION 7 Vector Cross Product Choose one . 4 points If a = (2, 1,0) and b = (1, 2, 1) , calculate a x b O axb =6 O a x b = (2, 2, 0) O axb = (1, -2,3)QUESTION 8 Vector Dot Product Choose one . 4 points if a = (-2, 1, 5) and b = (1, 2, 1) , calculate a - b O a - b = 5 O a - b = (-2, 2, 5) O a - b =9 QUESTION 9 Basis of a Matrix Row Space Choose one . 4 points 3 Find the basis of row space of matrix A = 1 . dim[rowsp(A)] and rank(A) O basis = {(1, 3, 1), (0, 5, 1)}, dim[rowsp(A)] = 2, rank(A) = 2 O basis = {(1, 3, 1), (0, 5, 1), (0, 0,0)}, dim[rowsp(A)] = 3, rank(A) = 3 O basis = {(1, 3, 1), (2, 1, 1), (5, 5,3)}, dim rowsp(A)] = 3, rank(A) = 3QUESTION 10 Transition Matrix between two bases Choose one . 4 points Consider the two bases below B= {ui, u2} = {(2, 1), (3, 1)} and B' = {vi, 12} = {(1, 1), (3,4) } Find the transition matrix from B to B' , MELB O 3 ME4 B= O 5 9 MELB= O 3 MB4 B= G 4QUESTION 11.2 Row Reduction Echelon Form Matrix Choose one . 4 points 3 Convert the following matrix A = -1 2 in reduced row echelon form(canonical -1 2 3 form) O 0 0 2 Tref(A) = 0 1 0 1 0 0 1 O 0 1 Tref(A) = 0 1 0 1 0 0 1 O 3 1 4 Tref( A) = 0 10 1 0 0 1QUESTION 11.3 Solution of a System of Linear Equations by Row Reduction Echelon Form Choose one . 4 points + 3y + Z 1 using the reduced row echelon form of its augmented Solve y + 2z E y + 2z = 3 matrix from the previous questions. O 1 =0, y=1,z=1 O 1 =1,y=2,2= -3 O 1 =2, y =1,2=-1V QUESTION 12 Matrix Addition Choose one . 4 points 0 2 1 2 0 5 Calculate 2.A - B* if A = 2 1 3 and B = -3 31 4 2 1 2 1 0 O 2 7 2 2.A - B' = 4 -1 5 3 3 4 O -2 2.A - B' = 4 -1 3 3 4 O -2 7 2A - B' = 4 -1 5 3 3 2\f\fQUESTION 14 Trace of matrix Choose one . 4 points 6 0 2 3 Find the trace of A = 5 7 2 3 9 6 O trace(A) = 6, 2,5, 6 O trace(A) = 17 O trace(A) = 19QUESTION 15 Transpose of a Matrix Choose one . 4 points 6 2 1 0' 0 2 Find the transpose of A = 5 7 5 -3 9 O 6 0 5 2 2 2 7 -3 5 9 3 7 7 O 6 0 5 2 2 2 7 -3 A = 1 5 9 3 7 6 O 0 2 6 A* = 2 -3 9 6 7 5V QUESTION 16 Order of a Matrix Choose one . 4 points 6 2 1 0 0 2 1 3 What is the order of A = 5 7 5 7 -3 9 O 16 O 4 O 4 x 4 V QUESTION 17 Linear independence using Matrix Echelon Form Choose one . 4 points Which vectors uj and uj are linear independent in IR? ? O wi = (3, 2), u2 = (6, 4) O wi = (1,4), u2 = (2, 1) O wi = (1, 1), u2 = (2, 2)GROUP 18 Partial Derivative of Vectors Group . 2 questions Given u = (ux, ly, uz) = (x'z+y, x+y, y+ >') answer the 2 questions below QUESTION 18.1 First partial Derivative of a Vector Choose one . 4 points Calculate or O = (2zz + y, 1 + y, y + z?) O = (2:zz, 0, 0) O = (2:zz, 1, 0)QUESTION 18.2 Second Partial Derivative of a Vector Choose one . 4 points Calculate O = (2x + y, 1 + y, y + 2z) = (21, 0, 0) O = (2:z, 1,0) V QUESTION 19 Vector Derivative Choose one . 4 points Given a = 2ti + 3t23 - k, calculate da da = (2, 3t, -1) O da dt = (2, 6t, -1) O da at = (2, 6t, 0)QUESTION 20 Vector Integration Choose one . 4 points Given a = 2ti + 3t27 - k, calculate f* a(t)dt O a(t) it = 8 + 26j - 2k O a(t) dt = 52 + 26j + 2k O a(t)dt - 8 + 26j + 2k