HELP!!! Please help me on this questions below and also draw graph too please and it's just one assignment which has this questions in it below those are little questions, please answer all of them correctly, don't have any questions left, I'm posting this by buying additional question please answer them correctly I really need to submit it by today, I don't need explanation you can just submit all questions answers below please you can Zoom in and able to see questions below clearly I do really appreciate your hardwork and time please help me to answer them correctly:)
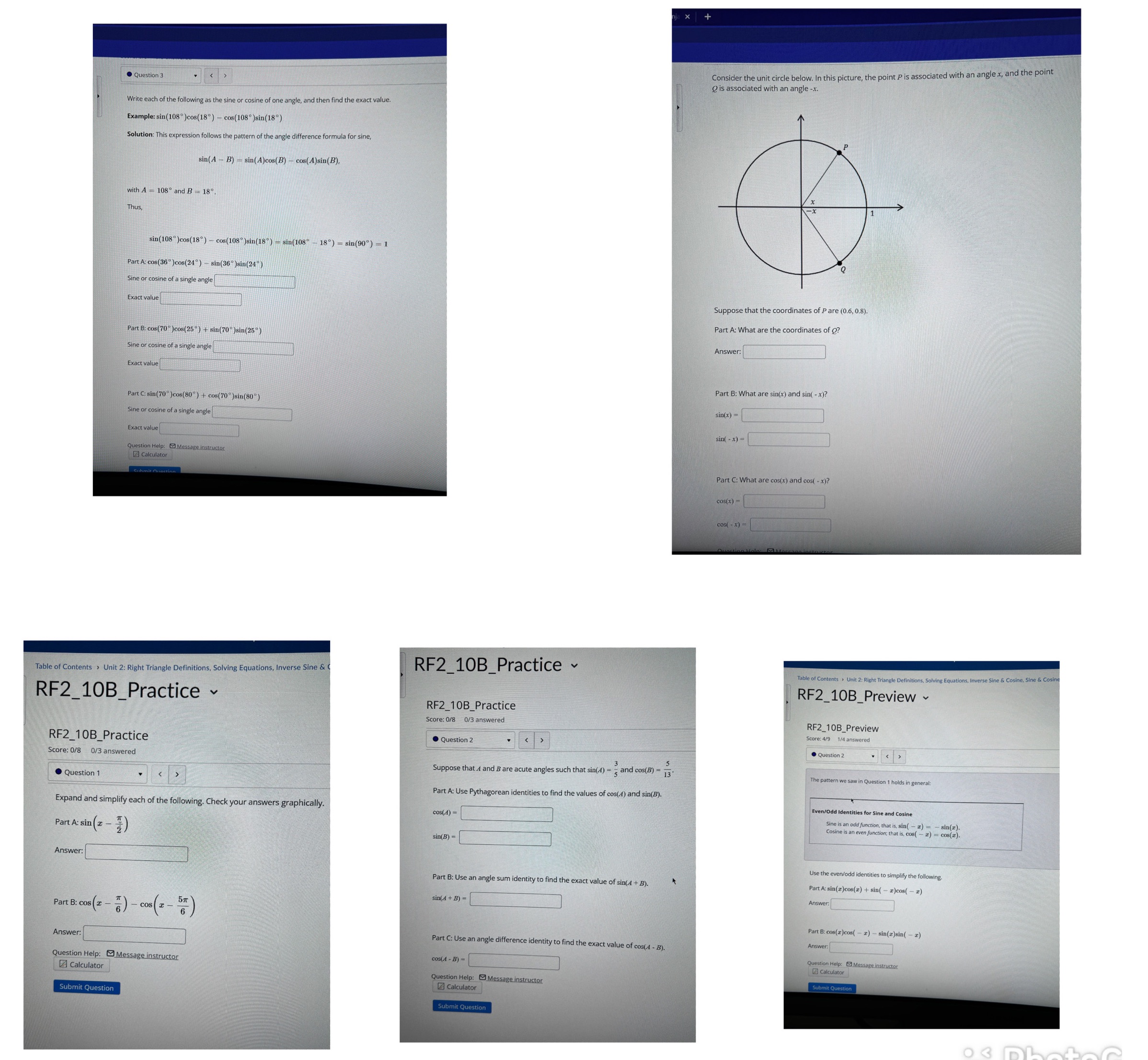
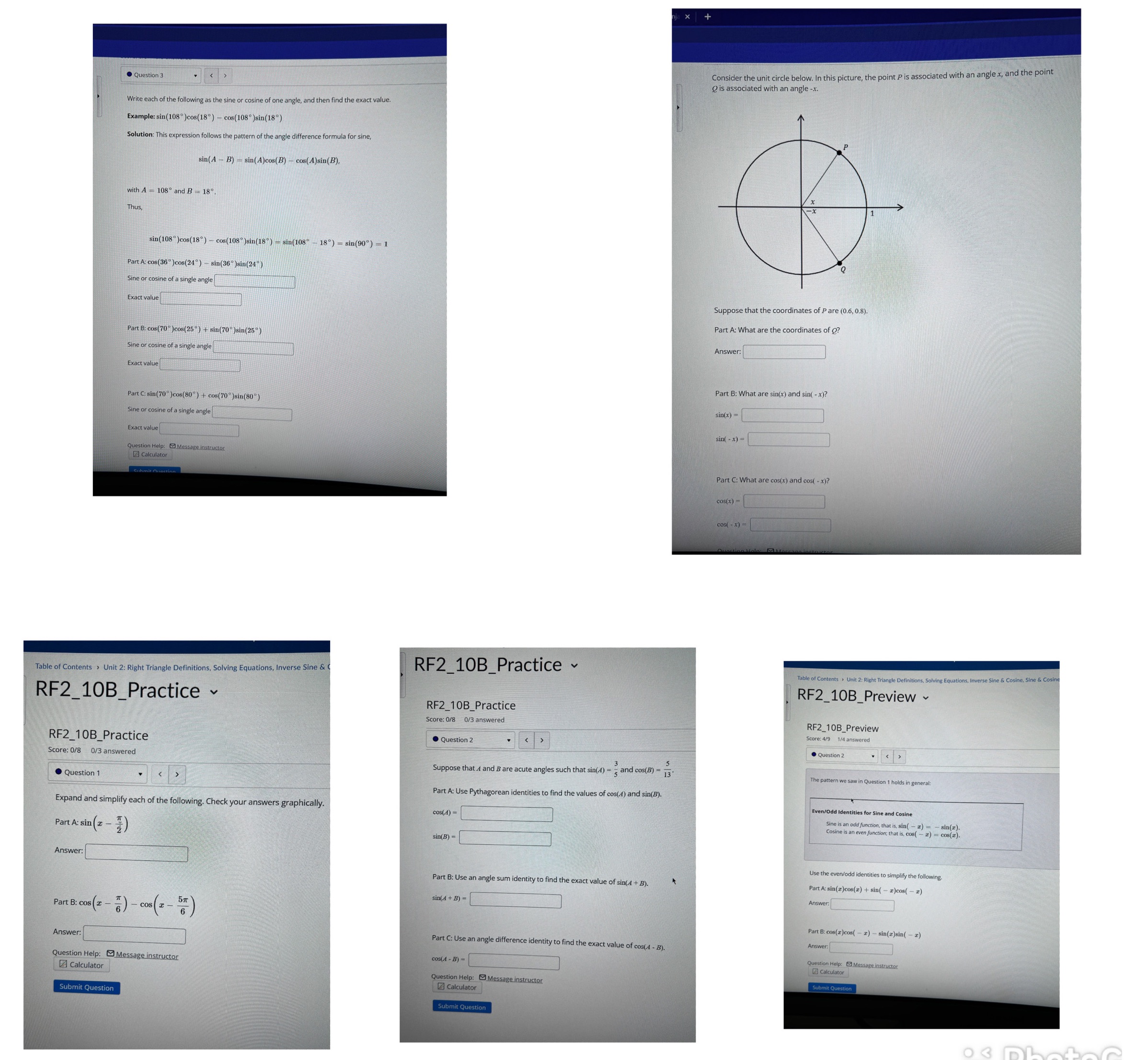
Consider the unit circle below. In this picture, the point P is associated with an angle x, and the point Question 3 @ is associated with an angle -x. Write each of the following as the sine or cosine of one angle, and then find the exact value. Example: sin(108 )cos(18) - cos(108 )sin(18") Solution: This expression follows the pattern of the angle difference formula for sine sin(A - B) - sin( A)cos(B) - cos( A)sin(B), with A = 108 and B - 18 Thus, sin(108)cos(18) - cos(108 )sin(18 ) -sin(108 -18) = sin(90) = 1 Part A: cos(36 )cos(24) - sin(36- )sin(24 ) sine or cosine of a single angle Exact value Suppose that the coordinates of P are (0.6, 0.8). Part A: What are the coordinates of ? Part B: cos(70 )cos(25*) + sin(70-)sin(25-) sine or cosine of a single angle Answer: exact value Part B: What are sin(x) and sin( -x)? Part C: sin(70 )cos(80) + cos(70 )sin(80) Sine or cosine of a single angle in(x) = Exact value sin( - x) - Question Help: Message instructor calculator Part C: What are cos(x) and cos( - x)? cos(x) = coS ( - x ) = able of Contents > Unit 2: Right Triangle Definitions, Solving Equations, Inverse Sine & RF2_10B_Practice Table of Contents > Unit 2 : Right Triangle Definitions , Solving Equations, Inverse Sine & Cosine, Sine & Cosin RF2_10B_Practice RF2_10B_Preview ~ RF2_10B_Practice Score: 0/8 0/3 answered RF2_10B_Preview RF2_10B_Practice . Question 2 Score: 4/9 1/4 answered Score: 0/8 0/3 answered . Question 2 Suppose that A and B are acute angles such that sin(4) - 5 and cos(B) - 13. . Question 1 the pattern we saw in Question 1 holds in general: Part A: Use Pythagorean identities to find the values of cos(4) and sin(B). Expand and simplify each of the following. Check your answers graphically. cos(A) = ven/Odd Identities for Sine and Cosine Sine is an odd function, that is, sin( - 2 Part A: sin (2 - ) Cosine is an even function ; that is , co( _sin(I). sin(B) = Answer: Use the even/odd identities to simplify the following. Part B: Use an angle sum identity to find the exact value of sin(A + B). art A: sin(z)cos(z) + sin( - z)cos( - I) nswer; Part B: cos (z - " ) - cos ( x - 5x ) sin(4 + B) = Part B: cos(z)cos( - z) - sin(z)sin( - z) Answer Part C: Use an angle difference identity to find the exact value of cos(A - B). Answer: Question Help: Message instructor cos(A - B) = uestion Help: Message instructor Calculator Calculator Question Help : Message instructor Submit Question Calculator Submit Question Submit