help please in python, this is what I have so far.


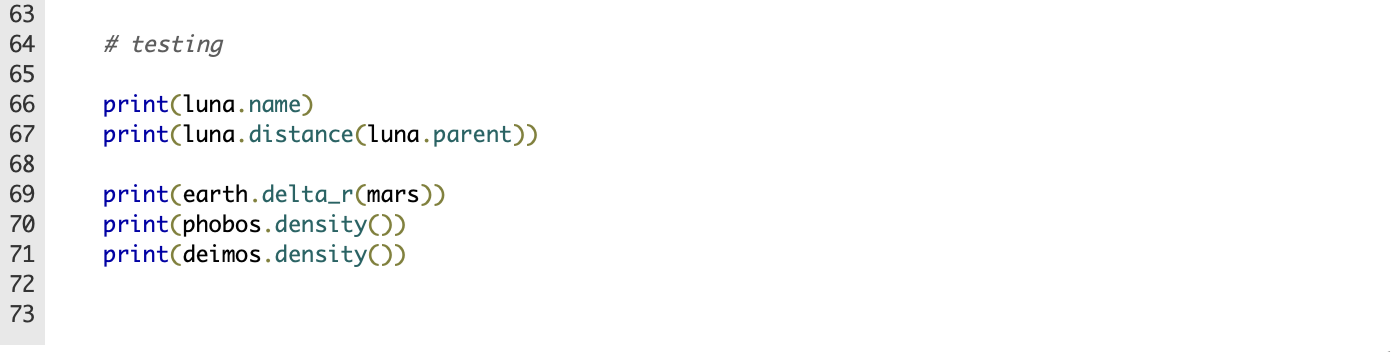
 This is all one question for the code
This is all one question for the code
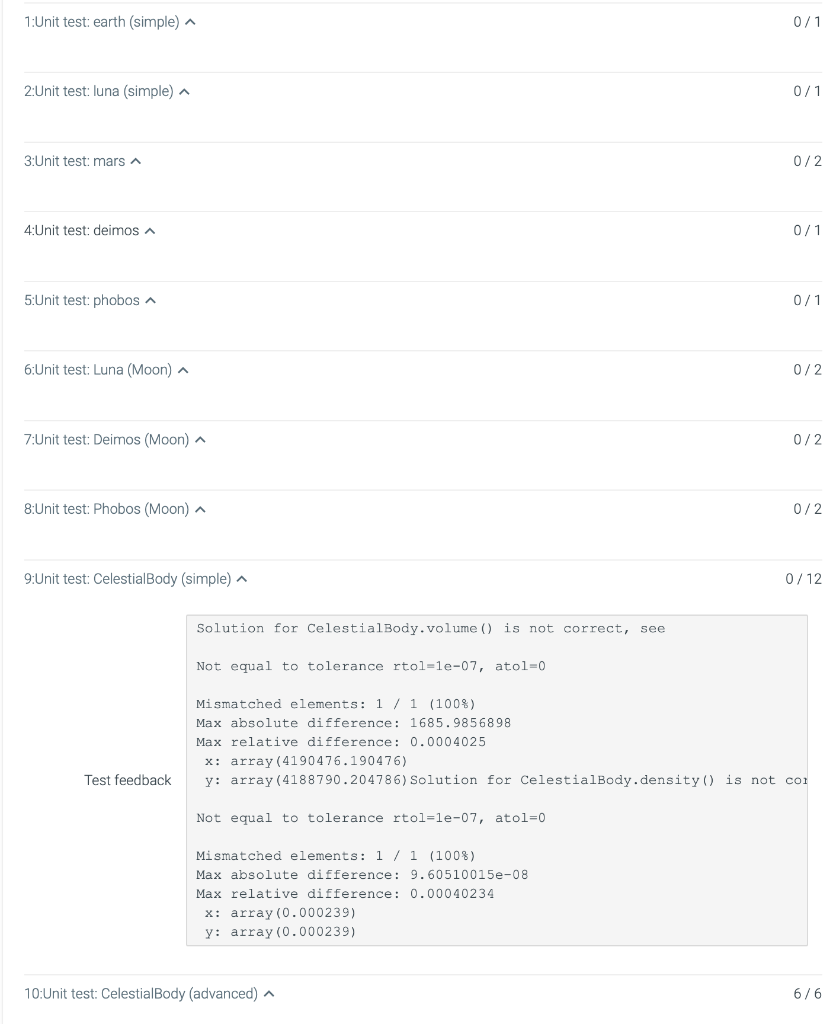
A simulation of the solar system would contain many different celestial bodies such as stars, planets, or moons. We want to approach the problem of keeping track of these bodies through an object-oriented approach where each body is represented by an instance of class of the type of body. In this problem you will create a base class CelestialBody and derive classes for Planet and Moon from the base class. You will then create instances for planet Earth (a Planet) and its moon Luna (a Moon) and planet Mars (Planet) and its moons Deimos (Moon) and Phobos (Moon). Base class CelestialBody Create a class CelestialBody. It should have the following attributes, which are all initialized with mandatory arguments in the order below when a new instance is created: - name: name of the body - position: a numpy array with the three cartesian coordinates in the coordinate system that has the center of mass of the solar system at its origin ("solar barycentric"), in astronomic units (AU) - mass: mass of the body in kg - radius: approximate radius in km The class should have the following methods: - volume ( ) : return the volume of the body (calculated as a sphere from the radius) - density ( ) : return the mass density (mass divided by volume) of the body - delta_r(other): The method takes another CelestialBody (or Planet or Moon) instance as an argument. It calculates and returns the cartesian difference vector (as a numpy array) pointing from itself to the other body. If the position of the body is r=(x,y,z) and the position of the other body is r=(x,y,z) then the difference vector is r=rr. - distance (other): Like delta_r( ), the method takes another CelestialBody instance as an argument and returns the distance between the two bodies as a float, d=rr where the inner product (scalar product or "dot product") between two vectors is used. Derived classes The class Planet should be derived from CelestialBody. Nothing else is required. (Hint: You can always add a pass into the body of the new class definition.) The class Moon should be derived from CelestialBody. It should be initialized with name, position, mass, radius, and the new argument parent. parent should be the planet, represented by a Planet, around which the moon orbits. Moon should have an attribute parent that stores the parent planet. Celestial objects Celestial objects Create the following objects (all data were obtained from the NASA HORIZON system): earth = Planet ( "Earth", np.array([9.978977040419635E01,6.586825681892025E02,6.320430920521123E5.97219e24,6371.01)luna=Moon("Luna",np.7.349array([9.956768547953816E01,6.676030485840675E02,1.641093070596718E04]),1737.53,earth) Also create mars and its moons deimos and phobos based on the following table (the radii for the moons are estimates because their actual shape is far from spherical). Note that Mars (as a Planet) does not have a parent so the entry in that column of the table was left empty: Testing The tests test the objects and their methods. For example, the following should work: Name of the Earth's moon: luna. name Distance between Luna and its parent, Earth: Iuna.distance (luna.parent) Direction from Earth to Mars: earth.delta_r(mars) Density of Phobos and Deimos phobos.density()deimos.density() (Note: we did not do customary unit conversion so the density is in kg/km3.) \# testing print(luna. name) print(luna. distance(luna.parent)) print(earth.delta_r(mars)) print(phobos. density()) print (deimos.density()) 1:Unit test: earth (simple) 0/1 2:Unit test: luna (simple) 0/1 3:Unit test: mars 0/2 4:Unit test: deimos 0/1 5:Unit test: phobos 0/1 6:Unit test: Luna (Moon) 0/2 7:Unit test: Deimos (Moon) 0/2 8:Unit test: Phobos (Moon) 0/2 9:Unit test: CelestialBody (simple) 0/12 10:Unit test: CelestialBody (advanced) ^ 6/6



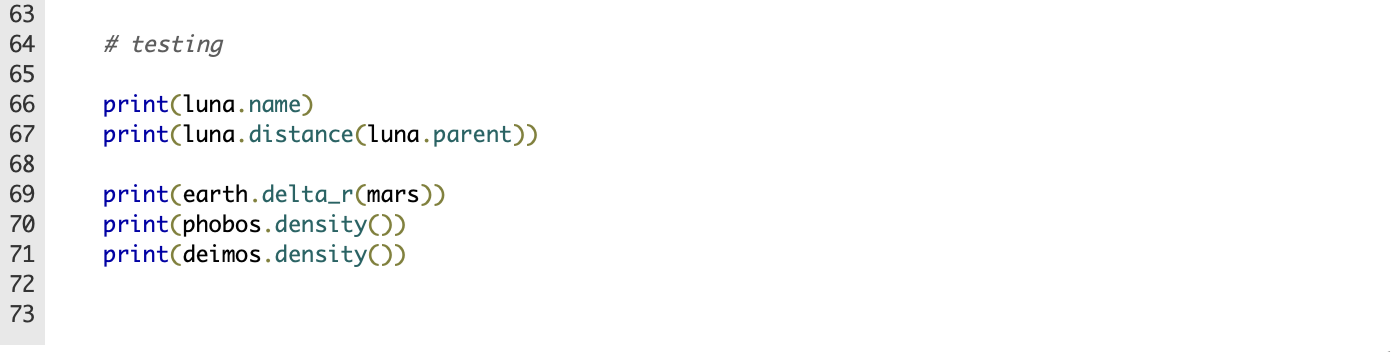
 This is all one question for the code
This is all one question for the code





