Help with C assignment

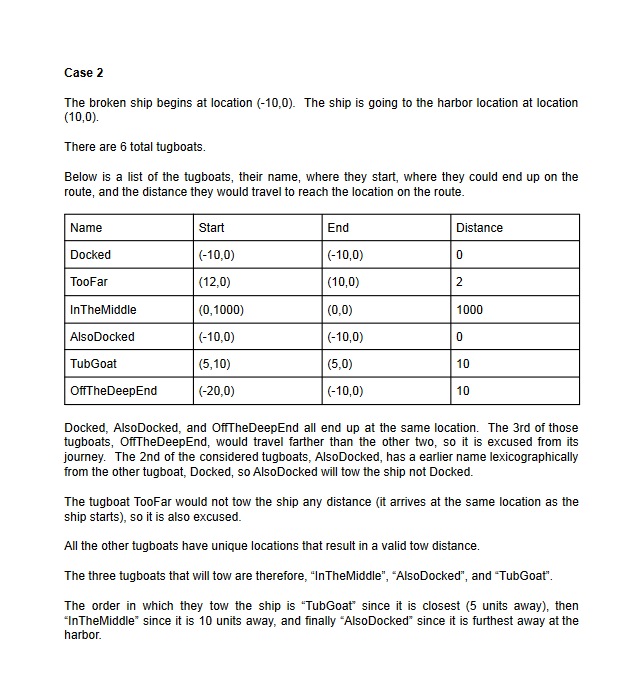
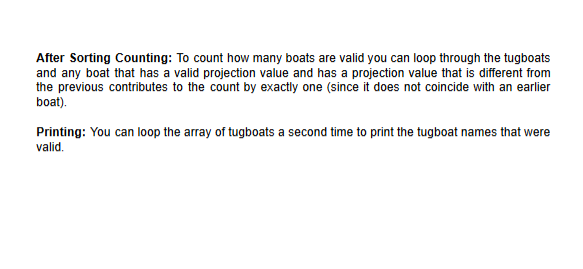
Tugboat Troubles Objective Give practice with sorting in C. Story The ship's engine has ceased, and now begins the preparations of taking the ship to the harbor for repairs. Luckily it's a straight shot to the harbor. The bad news is that the journey is long. There are several tugboats currently scattered throughout the ocean that can help move the ship to the harbor, but they may have to go out of their way to assist, and taking your crippled ship the full distance is going to be taxing on resources for any 1 particular tugboat. The tugboats have made an agreement. The tugboats will take the shortest path to the direct route that your ship will travel. Once the tugboats are on the route the closest tugboat to your ship will travel from its starting location on your ship's route to your ship's current location. Then the tugboat will tow your ship back to where the tugboat started on your ship's route. When your ship reaches that tugboat's starting location, the tugboat will stop towing your ship and will move back to its original location. After which the process will repeat with the next closest tugboat. If multiple tugboats would arrive at the same location on the ship's route, then only the tugboat that is closest to the location on the ship's route would move to that location. If multiple tugboats are the same distance from the location on the ship's route, then the tugboat with the lexicographically earliest name would move to the route. It is dangerous on the high seas, and you're afraid that your ship may fall victim to pirates that are pretending to be a valid tugboat. Your goal is to produce the names of the tugboats that will tow your ship to the harbor in the order they tow so that your ship. Problem Given the current location of your broken ship, the location of the harbor, and a list of tugboats with both their location and name, determine the number and order in which the tugboats will tow your ship based on the behavior specified above. Input Input will begin with a line containing 4 integers, xs,,ys,xn, and yn(10sxs,ys,xn,yn10s), representing the x and y coordinates of your ship and the x and y coordinates of the harbor respectively. The following line will contain a single integer, n(1n500,000), representing the number of tugboats. The following n lines will each contain a tugboat description (one per line). The tugboat description will contain 2 integers, x and y(10x,y10s), representing the x and y coordinates of the tugboat respectively, followed by a string, s, representing the name of the tugboat. The name will contain only upper and lower case characters of which there will be at most 20 . There will be at least 1 tugboat at the location of the harbor. Your ship does not start at the harbor. Output Output should begin with a number k, representing the number of tugboats that will tow your broken ship. Following this should be k lines each containing a single name of a tugboat, the full list comprise the list of the tugboats that will tow your ship in the order they tow your ship. Explanation Case 1 The broken ship begins at location (0,0). The ship is going to the harbor located at location (12,8). The next line states that there are 4 tugboats in the ocean. The tugboats are at locations (10,2),(0,13),(12,8), and (7,9). The names of the boats were ShipOnTheWater, KnotGonnaHelp, SailingPeacefully, and ADerelictBoat Tower. If the ship were to move onto the line that passes between the points (0,0) and (12,8), then - The first tugboat (ShipOnTheWater) would end up at point (6,4) - The second tugboat (KnotGonnaHelp) would end up at point (6,4) - The third tugboat (SailingPeacefully) would end up at point (12,8) - The fourth tugboat (ADerelictBoatTower) would end up at point (9,6) The first and second tugboat have their location coincide. Only 1 will tow the ship. The first tugboat is a distance of 42+62=52 units from the location on the route (6,4). The second tugboat is a distance of 62+92=117 units from the location on the route (6,4). The first tugboat is closer than the second tugboat, so the second tugboat will not move to the route that the ship will take from its starting location to the harbor. The third tugboat is on the harbor and does not have the same location as another ship, so it will tow the ship during the final leg of the journey. The fourth tugboat arrives at (9,6). It is the only boat to reach that location, and that location is on the route. It will also tow the ship at some point. The tugboat locations and the path they take to the route can be visualized with the following picture. The numbers represent the order in which the tugboat appears in the input. There are only 3 tugboats that will be used. The order of the tugboats that will be used is first (6,4), fourth (9,6), and third (12,8). The tugboat at position 1 will move to the line at position A to haul the broken ship to point A. Then tugboat 4 will haul the broken ship for the second leg of the journey. Finally tugboat 3 will haul the broken ship for the final leg of the journey. The ship names are ShipOnTheWater, ADerelictBoatTower, and SailingPeacefully Case 2 The broken ship begins at location (10,0). The ship is going to the harbor location at location (10,0) There are 6 total tugboats. Below is a list of the tugboats, their name, where they start, where they could end up on the route, and the distance they would travel to reach the location on the route. Docked, AlsoDocked, and OffTheDeepEnd all end up at the same location. The 3rd of those tugboats, OffTheDeepEnd, would travel farther than the other two, so it is excused from its journey. The 2nd of the considered tugboats, AlsoDocked, has a earlier name lexicographically from the other tugboat, Docked, so AlsoDocked will tow the ship not Docked. The tugboat TooFar would not tow the ship any distance (it arrives at the same location as the ship starts), so it is also excused. All the other tugboats have unique locations that result in a valid tow distance. The three tugboats that will tow are therefore, "InTheMiddle", "AlsoDocked", and "TubGoat". The order in which they tow the ship is "TubGoat" since it is closest (5 units away), then "InTheMiddle" since it is 10 units away, and finally "AlsoDocked" since it is furthest away at the harbor. Hints Use a Struct: Store the tugboats in a struct. Use an array of struct to hold all the tugboats, and sort the array. Comparator Function: Write a function that can return a value (e.g. 1 or 1 ) to represent the comparison between 2 tugboats. Avoid Floating Points: All the computations can be done without floating point data types (i.e. floats and doubles) using some "simple" vector geometry. I recommend using integer-like data types for holding the necessary data. Explanations as to how to do this follows in the primer below. High Precision: Using an int might not get enough precision based on the computations that will be done. I recommend using long long ints to hold on to your values during operations. For example consider using the following to create 2 long long ints COMPARISONS: There are 3 comparisons NEEDED for sorting your value. They are described in detail below. Geometry Primer Reorientation: It is INCREDIBLY useful to represent all your points with respect to the ship starting location. To do this you can subtract from all the points you have (harbor and tugboat locations) the location of your ship. That is decrement all the x coordinates by the ship's x coordinate and decrement all the y coordinates by the ship's y coordinate. Vector Point Duality: A vector is data with a magnitude and direction. In 2D space a vector can be expressed using an x and y component. A point has an x and y component, so points and vectors can be thought of as the same thing. The terms point and vector will be used interchangeably in the remainder of this primer. The Main Vector: The vector you will work with the most for this assignment is the one from the boat to the harbor. Since you should have already reoriented the points with respect to the ship's starting location, this vector will be the resulting location of the harbor. Point Line Projection: To find where a point lies on a line (represented by a vector) by moving the shortest distance possible can be found using projection. Below is an example of a projection (blue vector) of a vector (black dashed) onto another (solid black). This projection can determine where a tugboat will end up when going to the route the broken ship will take to the harbor. The projection of a point onto can be found using the dot product of 2 vectors. The dot product of 2 vectors is the sum of the products of their components dot(v1,v2)=v1xv2x+v1yv2y The reason why this helps is that the dot product of 2 vectors returns a value that represents the product of the magnitude of the 2 vectors multiplied by the cosine of the angle between the 2 vectors. The cosine of an angle represents the ratio of the adjacent with respect to the hypotenuse of a right triangle with that particular angle. The actual projection of v1 onto v2 is (dot(v1,v2)/magnitude(v2))normalized(v2) For this problem we care more about comparing the distances of these projections for sorting the points. The actual projections onto the line are not actually required. For this reason we can ignore BOTH the normalized vector v2 AND dividing by the magnitude of v2. We only need to consider the dot product, since all tugboats will be projected onto the same vector. Removing Tugboats that Don't Tug: There will be tugboats that are not actually going to move our ship anywhere. These tugboats will be the ones that have a non-positive projection (dot product), since they would be behind our line, OR ones that have a dot product whose value is more than the projection of the harbor (reoriented with respect to the ship's starting location) onto the main vector (the vector from the boat to the harbor). Optional Note: That the dot product of a vector with itself is the square of its magnitude. First Comparison Summary: The first value that should be compared when sorting the tugboats is the dot product of the main vector (vector from ship to harbor) with each tugboat vector (vector from ship to tugboat). Tie Breaking: If 2 tugboats have the same dot product, the tie is broken by determining which one moves the least distance to the line. I won't get into too many gory details in this primer, but there is a simpler method. Rather than checking the distance from the tugboat to the projection on the line (the point the tugboat will reach on the route), instead the distance from the tugboat to the ship can be used instead. The reason being how the square hypotenuse of a right triangle is equal to the sum of the squares of the legs of the right triangle. Well the vector from ship to tugboat is a hypotenuse of the vector from ship to projection and vector from projection to tugboat. Since 2 tugboats that arrive at the same project have an identical side length the other side length can be compared by using the hypotenuse instead. Distance Formula: To compute the distance to a point we use the following x2+y2 Where delta x and delta y are the change in x and y respectively. Avoiding Square Roots: The square root does not need to be taken since the square root is an increasing function for positive values. That means that if the square of a positive number is larger than the square of another positive number, then the first number must also be larger than the second. Second Comparison Summary: The second value that should be compared when sorting the tugboats is the square of the distance from the broken ship to the tugboat. END OF GEOMETRY PRIMER Final Comparison: You need to break ties between ships that have identical first and second values by the names themselves. You can use strcmp to compare 2 strings. After Sorting Counting: To count how many boats are valid you can loop through the tugboats and any boat that has a valid projection value and has a projection value that is different from the previous contributes to the count by exactly one (since it does not coincide with an earlier boat). Printing: You can loop the array of tugboats a second time to print the tugboat names that were valid. Grading Criteria - Good comments, whitespace, and variable names - 15 points - Use standard input/output - No extra input output (e.g. input prompts, "Please enter the number of friends:") - 5 points - Store an array of tugboats - Compare first by the distance from the ship to the tugboat projection (or equivalent) - 5 points - Break ties first by the distance from the tugboat to the projection (or equivalent) - 5 points - Break ties using a string comparison 05 points - After sorting loop through the array of tugboats a constant number of times (preferably twice) 5 points - Programs will be tested on 10 cases - 5 points each No points will be awarded to programs that do not compile using "gcc -std=gnu11 - m ". Sometimes a requested technique will be given, and solutions without the requested technique will have their maximum points total reduced. For this problem use your own sorting method. Without this programs will earn at most 50 points! I recommend vou use merge sort. You can use mv code as a base. DO NOT USE A BUILT IN SORTING METHOD Any case that causes a program to return a non-zero return code will be treated as wrong. Additionally, any case that takes longer than the maximum allowed time (the max of {5 times my solutions time, 10 secondsy) will also be treated as wrong. No partial credit will be awarded for an incorrect case