Help with C implementation of Karatsuba multiplication

UPDATED WITH MORE INFO AND SOURCE CODE

In this exercise we are working with relatively large integers (191 to 382 bits) which can not be stored inside a single data type in C. Therefore, we store them inside the arrays of unsigend long long data type (each element of array is 64-bits long) using radix-216 representation. a and b values are given in the following source code.

In product scanning method, you should compute each element of result array based on input indexes, i.e, we scan inputs based on each element of product. For the element of 0, we only scan a[0] and b[0] and compute the product of them. For the element of 1, we scan a[0], a[1], b[0] and b[1], multiply a[0] and b[1], multiply a[1] and b[0], and add the results to compute res[1]. You perform this procedure till you compute res[2n], where n is the input precision count: (Hint: you can simply implement this method using two for loops) r[0] = a[0] b[0] r[1] = a[0] b[1] + a[1] b[0] r[2] = a[0] b[2] + a[1] b[1] + a[2] b[0] ...

typedef unsigned long long bigint192[12]; //for operands typedef unsigned long long bigint384[24]; //for multiplication result

void bigint192_karatsuba_mul(bigint384 r, const bigint192 a, const bigint192 b)//complete this function { int i, j; long long ma[6], mb[6], z2[12], z1[12], z0[12]; //initialize arrays to 0 here //low multiplication z0 for (i = 0; i

void bigint192_print(const bigint192 a) { int i; printf("("); for (i = 0; i

}

Reference material:

The one level Karatsuba multiplication allows you to compute the product of two 191-bit integer a and b using three multiplications of smaller numbers, each with about half as many digits as a and b, plus some additions and digit shifts. In this exercise, a and b are represented using 12-digits in radix-216 representation. One can write the two given numbers as b = a1296 + a2 and b = b1296 + b2. Now the product can be computed as: a b = (a1296 + a2)(b1296 + b2) = z22192 + z1296 + z0 where z2 = a1b1 z1 = a1b0 + a0b1; 2 z0 = a0b0 Karatsuba observed that one can compute z1 using z2 and z0 as z1 = (a1 + a0)(b1 + b0) - z2 - z0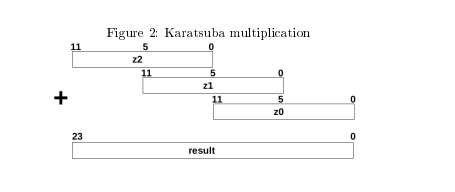

Figure 2: Karatsuba multiplication z1 z0 23 result Figure 2: Karatsuba multiplication z1 z0 23 result